Курсовая работа: Методы решения задач линейного программирования с n-переменными
Рис. 6 Выбираем отчет по результатам
Выбираем создание отчёта по результатам. Отчеты по устойчивости и пределам не создаются при использовании целочисленных ограничений на переменные. После нажатия кнопки OK в рабочей книге появляется новый лист с названием Отчет по результатам, содержащий отчёт по результатам, и получаем следующие результаты:
| Товар | Кол-во | Прибыль |
| A | 0 | 0 |
| B | 1061 | 53050 |
| C | 0 | 0 |
| D | 257 | 10280 |
| Стоимость продукции | 63330 | |
Рис. 7 Результат выполнения поиска решения
Отчет по результатам
| Microsoft Excel 11.0 Отчет по результатам | |||||
| Рабочий лист: [Лююю.xls]Лист1 | |||||
| Отчет создан: 15.02.2011 11:47:21 | |||||
| Целевая ячейка (Максимум) | |||||
| Ячейка | Имя | Исходное значение | Результат | ||
| $C$16 | Стоимость продукции Прибыль | 63337,32057 | 63330 | ||
| Изменяемые ячейки | |||||
| Ячейка | Имя | Исходное значение | Результат | ||
| $B$12 | A Кол-во | 0 | 0 | ||
| $B$13 | B Кол-во | 1061,004785 | 1061 | ||
| $B$14 | C Кол-во | 0 | 0 | ||
| $B$15 | D Кол-во | 257,1770335 | 257 | ||
| Ограничения | |||||
| Ячейка | Имя | Значение | Формула | Статус | Разница |
| $A$20 | Расход рабочего времени на единицу товара, ч | 969,92 | $A$20<=$F$3 | не связан. | 0,08 |
| $B$20 | Использование площади торгового зала на единицу товара, м2 | 289,96 | $B$20<=$F$4 | не связан. | 0,04 |
| $B$15 | D Кол-во | 257 | $B$15>=0 | не связан. | 257 |
| $B$14 | C Кол-во | 0 | $B$14>=0 | связанное | 0 |
| $B$12 | A Кол-во | 0 | $B$12>=0 | связанное | 0 |
| $B$13 | B Кол-во | 1061 | $B$13>=0 | не связан. | 1061 |
| $B$12 | A Кол-во | 0 | $B$12=целое | связанное | 0 |
| $B$13 | B Кол-во | 1061 | $B$13=целое | связанное | 0 |
| $B$14 | C Кол-во | 0 | $B$14=целое | связанное | 0 |
| $B$15 | D Кол-во | 257 | $B$15=целое | связанное | 0 |
Ответ: Чтобы прибыль максимальной – 63330 денежных единиц, предприятие должно выпустить 0 изделий товара A, 1061 изделий товара B, 0 изделий товара C и 257 изделий товара D.
линейное программирование прибыль товарооборот
Решение задачи графическим методом
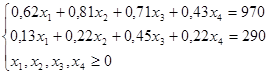
![]()
Задача решается графическим методом, если разность между количеством переменных и количеством ограничений равна двум.
n=4 (количество переменных)
m=2 (количество ограничений)
n -m=4-2=2
Выразим две переменные:
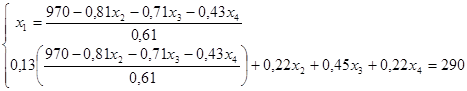
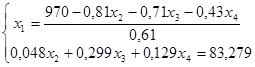
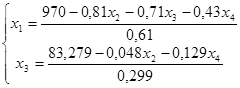
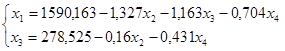
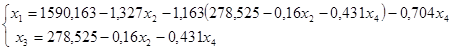
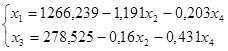
Подставим значения переменных в целевую функцию.
![]()
![]()
Найдем координаты прямых.
I. 1266,239-1,191x2 -0,203x4 =0
1,191x2 +0,203x4 =1266,239
x2 =1063,172-0,17x4
| x2 | 1063,172 | 893,172 |
| x4 | 0 | 1000 |
II. 278,525-0,16x2 -0,431x4 =0
0,16x2 +0,431x4 =278,525