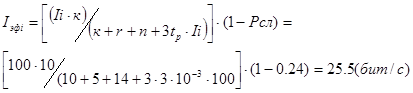Курсовая работа: Многоканальная система передачи информации

Как показали расчеты вероятность появления битовой ошибки при кодировании кодами Хэмминга Р _{b кх} тем меньше, чем больше основание кода m , т.е.чембольшее количество проверочных символов вводится в информационный сигнал.

Рассчитаем, оптимальные параметры кода Хэмминга (с точки зрения обеспечения СПДИ наименьшей вероятностью Р _{b кх} ). С этой целью рассчитаем количество контрольных бит r , которое можно ввести в систему, исходя из того, что при расчетах пропускной способности канала связи (КТЧ) и информационной производительности СПДИ было получено соотношение или иначе

(4.14)

Как было рассчитано ранее в (3.9):

Подставим в предыдущее выражение вместо С_к значение ∆С_к

Выразим и рассчитаем

-

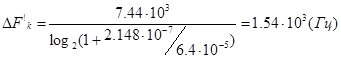эквивалентную ширину полосы пропускания.

Используя последнюю формулу, выразим r^! – количество бит четности, которые можно ввести в кодовое слово в передаваемом сигнале (исходя из условия, что пропускная способность канала ТЧ – главный сдерживающий фактор увеличения возможного числа проверочных бит и как следствие этому - повышения помехоустойчивости системы):

.

где T _б – длина одного тактового импульса.

Таким образом, в заданных условиях функционирования СПДИ, оптимальным количеством проверочных битов на каждый блок исходного сообщения кода Хэмминга, при котором вероятность появления битовой ошибки Pb _кх будет минимальной , а среднее время безошибочной работы М-го канала телеметрии будет максимальным станет равным r ^! = r =5 . В связи с этим, так как по условию к=10 (бит) , то n = k + r =15 (бит). Код Хэмминга в этом случае будет иметь вид, показанный для m=4, а именно , причем 1 бит из k бит кодового слова имеет смысл маркера кадра системы синхронизации, которая будет рассмотрена ниже.

Помехоустойчивое кодирование кодами Хэмминга, как показали расчеты, приводит к необходимости решения компромисса в СПДИ: кодирование с коррекцией ошибок требует избыточности, следовательно, увеличения скорости передачи информации и конечно увеличения полосы пропускания системы. Иными словами, в нашем случае, при кодировании кодом Хэмминга с параметрами (15,11) помехоустойчивость СПДИ увеличилась в 1.25 раза, т.е. , производительность СПДИ I_c увеличилась примерно в 1.93 раза и стала сопоставима с пропускной способностью канала ТЧ, т.е. .

Схема кодера, удовлетворяющего условию (15,11) приведена на рис.4.1

Рис.4.1 Схема кодера, удовлетворяющего условию (15,11).

Схема декодера, удовлетворяющего условию (15,11) приведена на рис.4.2

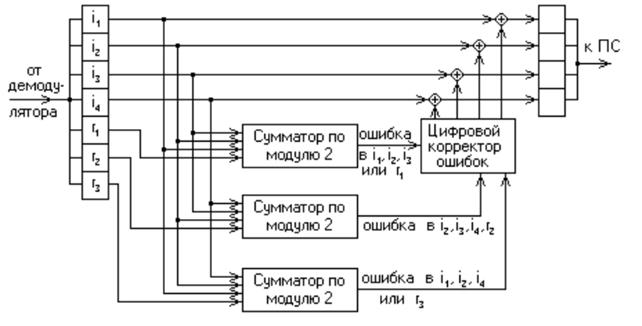
Рис.4.2 Схема декодера, удовлетворяющего условию (15,11).

4.2 Определение эффективной скорости приема сигналов данных и оптимальной длины передаваемых слов

Для обеспечения заданной достоверности при передаче данных наряду с помехоустойчивым кодированием применяют обратные связи, использование которых также приводит к появлению избыточности и, следовательно, к уменьшению скорости передачи данных.

Эффективная скорость I _{эф i} источника информации (или всей СПДИ I _эфСПДИ )показывает,как изменится скорость передачи исходного сообщения источника (группового сигнала системы) в канале связи, и зависит от состояния канала связи, оптимальной длины передаваемых слов, числа служебных разрядов, а также типа обратной связи. Как уже было сказано, в канале переспроса рассматриваемой СПДИ действует решающая обратная связь в виде однобитовых посылок импульсов. Поэтому выражение для I _{эф i} будет иметь вид:

(4.15)

Для кода Хэмминга вида (15,11) составляющие выражения (4.15) будут иметь значения: n_сл =15-1=14 (бит) – разница между общим числом бит слова прямого канала и канала переспроса (n _кп =1 ); к=10 (бит) иr =5 (бит); Ii – информационная производительность источника информации, Р _{b пк} – битовая вероятность ошибки в канале при применении кода (15,11), вероятность ошибки в принятом слове Р_сл .

(4.16)

При этом необходимо учитывать время распространения сигналов по каналу t _p . Примем - для стандартного КТЧ все параметры нормируются к длине канала l =1000 (км) ; с – скорость распространения радиоволны.

Таким образом, рассчитаем :