Курсовая работа: Модель распределения ресурсов

Приведенный пример многошаговой операции показывает, что управление на каждом шаге надо выбирать с учетом его последствий на предстоящих шагах. Это основное правило ДП, сформулированное Р. Беллманом, называется принципом оптимальности.

Оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.

Использование этого принципа гарантирует, что управление, выбранное на любом шаге, является не локально лучшим, а лучшим с точки зрения процесса в целом.

Так, если система в начале k-го шага находится в состоянии , и мы выбираем произвольное управление , то система придет в новое состояние , и дальнейшие управления должны выбираться оптимальными относительно состояния . Последнее означает, что при этих управлениях максимизируется показатель эффективности на последующих до конца процесса шагах k +1,...,n , т. е. величина . Показатель, характеризующий суммарную эффективность от данного k-го до последнего п-го шага, будем обозначать через , т.е. . Задача оптимизации процесса, начиная с k -го до последнего n -го шага (рис. 3), похожа на исходную при начальном состоянии системы , управлении и показателе эффективности [аналогично (1.2)]. Выбрав оптимальное управление на оставшихся п— k +l шагах, получим величину , которая зависит только от , т. е.

. (1.4)

Назовем величину условным максимумом . Если теперь мы выберем на k -м шаге некоторое произвольное управление , то система придет в состояние . Согласно принципу оптимальности, какое бы мы ни выбрали, на последующих шагах управление должно выбираться так, чтобы показатель эффективности достигал максимального значения, равного . Остается выбрать управление . Его нельзя выбирать из условия локальной максимизации показателя эффективности на данном k -м шаге, лишь бы получить . Такой подход был бы недальновидным, поскольку от выбора зависит новое состояние , а от последнего—максимально возможная эффективность, которая может быть достигнута в дальнейшем, т. е. величина . Поэтому необходимо выбирать управление так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k +1)-го) приводило бы к общему максимуму показателя эффективности на п—k +l шагах, начиная с k -го до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:

, (1.5)

получившего название основного функционального уравнения ДП , или уравнения Беллмана . Схематически соотношение (1.5) иллюстрируется на рис. 3.

Рисунок 3

Из уравнения (1.5) может быть получена функция , если известна функция ; аналогично можно получить , если найдена и т. д., пока не будет определена величина , представляющая по определению максимальное значение показателя эффективности процесса в целом: .

Соотношения (1.5) для определения последовательности функций через получили название основных рекуррентных уравнений Беллмана .

Решая уравнение (1.5) для определения условного максимума показателя эффективности за n —k +l шагов, начиная с k -го, мы определяем соответствующее оптимальное управление , при котором этот максимум достигается. Это управление также зависит от . Будем обозначать такое управление через и называть условным оптимальным управлением на k-м шаге .

Основное значение уравнения (1.5), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения - максимума функции (1.2) n переменных , ,…, сводится к решению последовательности n задач, задаваемых соотношениями (1.5), каждое из которых является задачей максимизации функции одной переменной . Эти задачи оказываются взаимосвязанными, так как в соотношении (1.5) при определении учитывается найденная при решении предыдущей задачи функция .

2. Оптимальное распределение ресурсов

2.1 Постановка задачи

Класс задач, рассматриваемый в данной главе, имеет многочисленные практические приложения.

В общем виде эти задачи могут быть описаны следующим образом. Имеется некоторое количество ресурсов, под которыми можно понимать денежные средства, материальные ресурсы (например, сырье, полуфабрикаты, трудовые ресурсы, различные виды оборудования и т. п.). Эти ресурсы необходимо распределить между различными объектами их использования по отдельным промежуткам планового периода или по различным промежутками по различным объектам так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, например, прибыль, товарная продукция, фондоотдача (задачи максимизации) или суммарные затраты, себестоимость, время выполнения данного объема работ и т. п. (задачи минимизации).

Вообще говоря, подавляющее число задач математического программирования вписывается в общую постановку задачи оптимального распределения ресурсов. Естественно, что при рассмотрении моделей и вычислительных схем решения подобных задач методом ДП необходимо конкретизировать общую форму задачи распределения ресурсов.

В дальнейшем будем предполагать, что условия, необходимые для построения модели ДП, в задаче выполняются. Опишем типичную задачу распределения ресурсов в общем виде.

Задача 1. Имеется начальное количество средств , которое необходимо распределить в течение n лет между s предприятиями. Средства , выделенные в k -м году i -му предприятию, приносят доход в размере и к концу года возвращаются в количестве. В последующем распределении доход может либо участвовать (частично или полностью), либо не участвовать.

Требуется определить такой способ распределения ресурсов (количество средств, выделяемых каждому предприятию в каждом плановом году), чтобы суммарный доход от s предприятий за n лет был максимальным.

Следовательно, в качестве показателя эффективности процесса распределения ресурсов за n лет принимается суммарный доход, полученный от s предприятий:

. (2.1)

Количество ресурсов в начале k -го года будем характеризовать величиной (параметр состояния). Управление на k -м шаге состоит в выборе переменных , обозначающих ресурсы, выделяемые в k -м году i -му предприятию.

Если предположить, что доход в дальнейшем распределении не участвует, то уравнение состояния процесса имеет вид

(2.2)

Если же некоторая часть дохода участвует в дальнейшем распределении в каком-нибудь году, то к правой части равенства (2.2) прибавляется соответствующая величина.

Требуется определить ns неотрицательных переменных , удовлетворяющих условиям (2.2) и максимизирующих функцию (2.1).

Вычислительная процедура ДП начинается с введения функции , обозначающей доход, полученный за п— k +1 лет, начиная с k-го года до конца рассматриваемого периода, при оптимальном распределении средств между s предприятиями, если в k -м году распределялось средств. Функции для удовлетворяют функциональным уравнениям (1.5), которые запишутся в виде

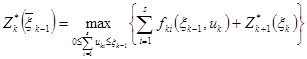(2.3)