Курсовая работа: Модель распределения ресурсов

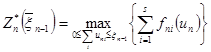. (2.4)

Далее необходимо последовательно решить уравнения (2.4) и (2.3) для всех возможных . Каждое из этих уравнений представляет собой задачу на оптимизацию функции, зависящей от s переменных. Таким образом, задача с ns переменными сведена к последовательности n задач, каждая из которых содержит s переменных. В этой общей постановке задача по-прежнему сложна (из-за многомерности) и упростить ее, рассматривая как ns-шаговую задачу, в данном случае нельзя. В самом деле, попробуем это сделать. Пронумеруем шаги по номерам предприятий сначала в 1-м году, затем во 2-м и т. д.:

и будем пользоваться одним параметром для характеристики остатка средств.

В течение k -го года состояние к началу любого шага (i =l, 2, .... s ) определится по предыдущему состоянию с помощью простого уравнения . Однако по истечении года, т. е. к началу следующего года, к наличным средствам необходимо будет добавить средств и, следовательно, состояние в начале -го шага будет зависеть не только от предшествующего ks -го состояния, но и от всех s состояний и управлений за прошлый год. В результате мы получим процесс с последействием. Чтобы исключить последействие, приходится вводить несколько параметров состоянии; задача на каждом шаге остается по-прежнему сложной из-за многомерности.

2.2 Двумерная модель распределения ресурсов

Задача 2. Планируется деятельность двух предприятий (s =2) в течение n лет. Начальные средства составляют . Средства x , вложенные в предприятие I, приносят к концу года доход и возвращаются в размере ; аналогично, средства x , вложенные в предприятие II, дают доход и возвращаются в размере . По истечении года все оставшиеся средства заново перераспределяются между предприятиями I и II, новых средств не поступает и доход в производство не вкладывается.

Требуется найти оптимальный способ распределения имеющихся средств.

Будем рассматривать процесс распределения средств как n -шаговый, в котором номер шага соответствует номеру года. Управляемая система — два предприятия с вложенными в них средствами. Система характеризуется одним параметром состояния — количеством средств, которые следует перераспределить в начале k -го года. Переменных управления на каждом шаге две: и — количество средств, выделенных соответственно предприятию I и II. Так как средства ежегодно перераспределяются полностью, то . Для каждого шага задача становится одномерной. Обозначим через , тогда .

Показатель эффективности k -го шага равен . Это—доход, полученный от двух предприятий в течение k -го года.

Показатель эффективности задачи—доход, полученный от двух предприятий в течение n лет—составляет

. (2.5)

Уравнение состояния выражает остаток средств после k -го шага и имеет вид

. (2.6)

Пусть — условный оптимальный доход, полученный от распределения средств между двумя предприятиями за п— k +1 лет, начиная с k -го года до конца рассматриваемого периода. Запишем рекуррентные соотношения для этих функций:

; (2.7)

,

где - определяется из уравнения состояния (2.6).

Задача 3. Решить задачу 2 при следующих условиях: ; ; ; ; ; .

Если и - средства, выделенные соответственно предприятиям I и II в k -м году, то суммарный доход, полученный от обоих предприятий, равен

,

а уравнение состояния (2.6) принимает вид

.

Основные функциональные уравнения (2.7) запишутся следующим образом:

;

.

Проведем этап условной оптимизации.

4-й шаг. Условный оптимальный доход равен

,