Курсовая работа: Моделирование геометрического паркета из пятиугольников и шестиугольников

1), (1)

2), (2)

3). (3)

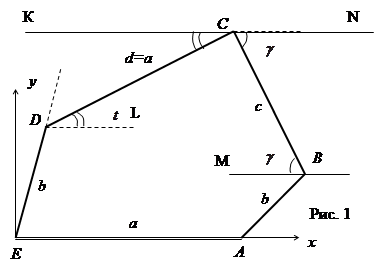
В классификации М. Гарднера [3, c.184], [1 , c. 196] и Марджори Райс [3, c.189] этому пятиугольнику присвоен тип № 2.

Условия (2) и (3) не являются независимыми. Вычисляя сумму углов пятиугольника по формуле , получаем 540⁰ , поэтому достаточно потребовать выполнение одного из условий (2), (3), тогда второе выполняется автоматически. Итак, уменьшая число параметров для пятиугольника на 2 на основании равенств (1), (3), получаем пять параметров для задания пятиугольника. Это (рис. 2.)

1) длины сторон: a = AE , b = ED , c = CB ,

2) углы: .

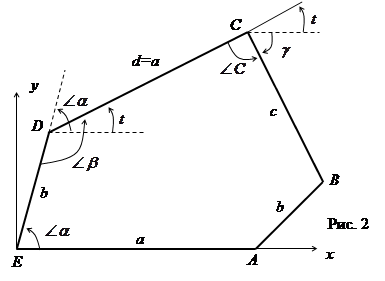Для декартовой системы координат, изображенной на рисунке 2, получаем координаты вершин и векторов:

.

Для задания вектора введем вспомогательный угол , образованный этим вектором с положительным направлением оси Ох

Для углов в точке D с учетом их ориентации имеем

или

Для задания вектора введем вспомогательный угол, образованный этим вектором с положительным направлением оси .

Для углов в точке С имеем

,

.

,

На вводимые параметры наложим естественные условия:

(4)

Но при построении пятиугольника с этими условиями могут возникнуть следующие конфигурации, приводящие к невыпуклым пятиугольникам:

а) После последовательного построения отрезков ЕА, ED , DC для пятиугольника точки Е и С оказались расположенными по одну стороны относительно прямой AD (рис. 2, рис. 3), но в выпуклом многоугольнике точки Е и С должны располагаться по разные стороны относительно диагонали AD .

Две точки расположены по одну сторону относительно прямой, заданной уравнением , тогда и только тогда, когда выполняется условие