Курсовая работа: Моделирование как метод разработки управленческого решения
– в условиях полной неопределённости;
– в условиях частичной определённости;
– в условиях эксперимента, предшествующего принятию решения;
– с применением аппарата решающих функций и использованием функции риска.
2.4 Решение задачи
Критерии принятия решений в условиях полной неопределённости.
Критерий Уолда
| Решение планового органа | Минимум выигрыша |
| А1 | -18 |
| А2 | 12* |
EY = maximinjeij
Максимаксный критерий
| Решение планового органа | Максимум выигрыша |
| А1 | 62* |
| А2 | 12 |
EM = maximaxjeij
Критерий Гурвича
| Решение планового органа | Степень оптимизма a | |||||||
| 0 | 0,2 | 0,3 | 0,4 | 0,6 | 0,8 | 1 | 0 | |
| А1 | -18 | -2 | 6 | 14 | 30 | 46 | 62 | -18 |
| А2 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
Критерий Сэвиджа
| Решение планового органа | Состояние природы | Максимум сожаления | ||
| В1 | В2 | В3 | ||
| А1 | 0 | 0 | 30 | 30 |
| А2 | 50 | 10 | 0 | 50 |
EC = mini maxj (maxi eij - eij)
Критерий Лапласа
Решение планового органа | Равновероятный выигрыш |
| А1 | 22* |
| А2 | 12 |
n
EЛ = maxi S ( eij / n)
j=1
Критерий принятия решений в условиях частичной определённости.
Условия частичной определенности предполагают, что распределение вероятностей состояний «природы» p(bj) известно и статистически устойчиво. В соответствии с исходными данными это распределение имеет вид:
p(b1) =0,25 p(b2) =0,50 p(b3) =0,25
Критерий Байеса-Лапласа
| Решение планового органа | Математическое ожидание выигрыша |
| А1 | 22* |
| А2 | 12 |
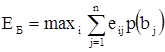
Принятие решений в статистических играх с экспериментом.
Принятию решения предшествует эксперимент. Допустим, что результаты эксперимента образуют множество X = {x1, x2, x3}, где исход эксперимента x1 означает, что проведение данной НИОКР потребует 5 лет, x2 – соответственно 10 лет и x3 – 15 лет. Как правило, такие результаты эксперимента носят не достоверный, а вероятностный характер. Это приводит к необходимости использования условных вероятностей p(xi/bj), которые показывают вероятность прихода к выводу xi, если на самом деле имеет место состояние «природы» bj.
В соответствии с исходными данными условные вероятности p(xi/bj) исходов эксперимента:
p(x1/b1) = 0,25 p(x1/b2) =0,80 p(x1/b3) =0,20
p(x2/b1) = 0,15 (x2/b2) =0,10 p(x2/b3) =0,70
p(x3/b1) =0,65 p(x3/b2) =0,25 p(x3/b3) =0,15
Находим полные вероятности исходов эксперимента:
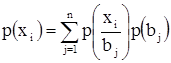
p(x1) = p(x1/b1)p(b1) + p(x1/b2)p(b2) + p(x1/b3)p(b3)
p(x2) = p(x2/b1)p(b1) + p(x2/b2)p(b2) + p(x2/b3)p(b3)
p(x3) = p(x3/b1)p(b1) + p(x3/b2)p(b2) + p(x3/b3)p(b3)
p(x1) = 0,25×0,25+0,80∙0,50+0,20∙0,25=0,5125
p(x2) = 0,15×0,25+0,10∙0,50+0,70∙0,25=0,2625
p(x3) =0,65×0,25+0,25∙0,50+0,15∙0,25=0,325