Курсовая работа: Моделирование как метод разработки управленческого решения

p(bj / xi) = p(xi / bj) p(bj) / p(xi)

p(b1/x1) = p(x1/b1)p(b1)/p(x1) =0,25∙0,25/0,5125≈0,1220

p(b2/x1) = p(x1/b2)p(b2)/p(x1) = 0,80∙0,50/0,5125≈0,7805

p(b3/x1) = p(x1/b3)p(b3)/p(x1) =0,20∙0,25/0,5125≈0,0976

p(b1/x2) = p(x2/b1)p(b1)/p(x2) =0,15∙0,25/0,2625≈0,1429

p(b2/x2) = p(x2/b2)p(b2)/p(x2) = 0,10∙0,50/0,2625≈0,1905

p(b3/x2) = p(x2/b3)p(b3)/p(x2) =0,70∙0,25/0,2625≈0,6667

p(b1/x3) = p(x3/b1)p(b1)/p(x3) = 0,65∙0,25/0,325=0,5

p(b2/x3) = p(x3/b2)p(b2)/p(x3) = 0,25∙0,50/0,325≈0,3846

p(b3/x3) = p(x3/b3)p(b3)/p(x3) =0,15∙0,25/0,325≈0,1154

Таким образом:

p(b1/x1) = 0,1220 p(b2/x1) = 0,7805 p(b3/x1) = 0,0976

p(b1/x2) = 0,1429 p(b2/x2) = 0,1905 p(b3/x2) = 0,6667

p(b1/x3) = 0,5 p(b2/x3) = 0,3846 p(b3/x3) = 0,1154

Находим по критерию Байеса-Лапласа (с учётом уже апостериорных вероятностей состояний «природы» p(bj / xi) ) ожидаемые выигрыши для каждого исхода эксперимента:

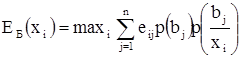
62∙0,1220+22∙0,7805+(-18)∙0,0976=22,97561* Þ А1

EБ (x1) = max

12∙0,1220+12∙0,7805+12∙0,0976=12

62∙0,1429+22∙0,1905+(-18)∙0,6667=1,047619

EБ (x2) = max

12∙0,1429+12∙0,1905+12∙0,6667≈12*Þ А1

62∙0,5+22∙0,3846+(-18)∙0,1154=39,6*Þ А2

EБ (x3) = max

12∙0,5+12∙0,3846+12∙0,1154=12

Средний выигрыш при неизвестном заранее исходе эксперимента равен:

= » 22,97561∙0,5125+12∙0,2625+39,6∙0,3125=27,3

При этом =27,3 > Е = 22 , то есть средний выигрыш с экспериментом больше, чем выигрыш без эксперимента.