Курсовая работа: Моделирование ПИД-регулятора и преобразователя давления в частоту в пакете LabVIEW
Моделирование преобразователя давления в частоту в пакете LabVIEW
Исходные данные.
Для набора экспериментально полученных данных (см. таблица 1) определить функциональную зависимость частоты от давления и реализовать ее в пакете LabVIEW.
Таблица 1. Экспериментальные значения зависимости частоты от давления.
| № | P (гПа) | F, кГц |
| 1. | 1,33322 | 8,337360278 |
| 2. | 2,66644 | 8,339212478 |
| 3. | 6,6661 | 8,344742683 |
| 4. | 13,3322 | 8,353939718 |
| 5. | 66,661 | 8,427137202 |
| 6. | 133,322 | 8,51769675 |
| 7. | 199,983 | 8,607303073 |
| 8. | 266,644 | 8,695851044 |
| 9. | 333,305 | 8,78350556 |
| 10. | 399,966 | 8,870260553 |
| 11. | 466,627 | 8,956132326 |
| 12. | 533,288 | 9,041130271 |
| 13. | 599,949 | 9,125279872 |
| 14. | 666,61 | 9,208631398 |
| 15. | 733,271 | 9,291168401 |
| 16. | 799,932 | 9,372910134 |
| 17. | 866,593 | 9,453914483 |
| 18. | 933,254 | 9,534191805 |
| 19. | 999,915 | 9,613761369 |
| 20. | 1066,576 | 9,692624581 |
| 21. | 1133,237 | 9,77080238 |
| 22. | 1194,898 | 9,848293926 |
| 23. | 1333,22 | 10,00133498 |
| 24. | 1466,542 | 10,15193693 |
| 25. | 1599,864 | 10,30011327 |
| 26. | 1733,185 | 10,44602217 |
| 27. | 1866,508 | 10,58966349 |
| 28. | 1999,83 | 10,73106266 |
| 29. | 2133,152 | 10,87046144 |
| 30. | 2266,474 | 11,00847094 |
| 31. | 2399,796 | 11,14505163 |
| 32. | 2533,119 | 11,27929759 |
Функциональную зависимость необходимо определить с помощью следующих методов:
1. Интерполяция методом наименьших квадратов;
2. Построение функции F(P), используя интерполяционный многочлен Лагранжа;
3. Построение функции F(P), используя интерполяционный многочлен Ньютона;
4. Построение функции F(P), используя кубические сплайны.
1. Интерполяция методом наименьших квадратов
Вычисления, связанные с нахождением функции зависимости методом наименьших квадратов, будем производить в пакете MathCad.
С помощью программирования в среде MathCad составим программу МНК, которая вычисляет коэффициенты полинома, реализующего необходимую нам зависимость.

Графики, построенные по экспериментальным данным, и полученного полинома:

интерполяция преобразователь регулятор давление частота
интерполяция преобразователь регулятор давление частота
Проверка:
2. Построение функции F(P), используя интерполяционный многочлен Лагранжа
Вычисления, связанные с нахождением функции F(P), используя интерполяционный многочлен Лагранжа, будем производить в пакете MathCad.
Для упрощения вычислений разделим все экспериментальные данные на 6 групп. И для каждой группы определим свой интерполяционный многочлен Лагранжа.
Например, для группы данных на участке от 9,083кГц до 9,574кГц:

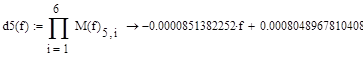 |
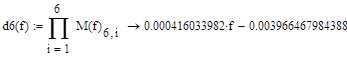 |
![]()
![]()
Искомый многочлен:
![]()
Графики, построенные по экспериментальным данным, и полученного полинома:
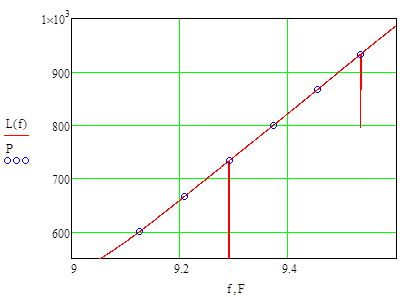 |
Проверка:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--