Курсовая работа: Моделирование SH-волны

.

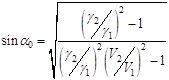При дальнейшем увеличении угла падения, когда , коэффициент отражения А стремительно возрастает от 0 при до 1, при одновременно и также быстро В растет от 1 до 2. Однако, более существенные изменения коэффициентов А и В и вторичных волн - отраженной и проходящей - происходят, когда угол падения становится больше критического. Если (напомним, ), в соответствии с законом Снеллиуса:

и

синус угле прохождения при закритическом падении становится больше единицы (?!). Это не может быть в области действительных тригонометрических функций. Определим косинус угле прохождения по обычной формуле:

, так как .

Синусу, большему 1, соответствует чисто мнимый косинус.

Встретившись с этой неожиданной трансформацией косинуса, мы, из осторожности, записали оба возможных знака (±) корня. Установим, какой из них имеет физический смысл. Для этого вспомним описание проходящей волны (в волновой аргумент которой и входит ) и ее спектра:

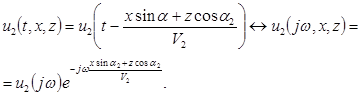
Подставим в последнее определение

:

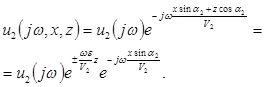
Наличие мнимой единицы в определении косинуса выводит зависимость от z из функции запаздывания и превращает ее в амплитудный множитель . Если определить , то с ростом z (то есть, при удалении от границы и от предполагаемого источника колебаний) амплитуда гармоники частоты ω неограниченно возрастает:

при z → ∞ .

Физически это абсолютно невозможно, поэтому из двух знаков мнимого косинуса следует выбрать минус: . Тогда амплитуда вторичной волны, определяемая множителем , стремится к нулю при удалении от границы (z → ∞).

Однако, спектр импульсного сигнала определен на всем бесконечном интервале частот: - ∞ ≤ ω ≤ ∞ и в волновом импульсе присутствуют как гармоники с положительными частотами, так и гармоники с ω < 0. Знак минус в определении “правильно действует" только для положительных частот. Для отрицательных частот знак минус гаснет и амплитуда гармоники частоты ω < 0 неограниченно возрастает по мере удаления от границы z → ∞. Это - снова нереально.

Чтобы обеспечить затухание всего спектра волны как для положительных, так и для отрицательных частот, определим:

,

где sgn (ω) - знаковая функция частоты:

.

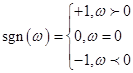В таком определении амплитудный множитель обеспечивает затухание гармонических составляющих со всеми частотами: если ω > 0, sgn (ω) = + 1 и - функция, убывающая с ростом z, если же ω < 0, sgn (ω) = - 1 и - так же убывающая по мере удаления от границы функция.

Обратим внимание на то, что с ростом абсолютного значения частоты ω затухание ускоряется - чем выше частота гармоники, тем быстрее она затухает с ростом z.

В функции запаздывания спектра проходящей волны осталась лишь пространственная переменная x: . Эта функция соответствует скольжению плоской волны вдоль границы со скоростью , меньшей истинной скорости волны в нижней среде, так как . Эта скользящая с “неправильной" скоростью волна имеет амплитуду, экспоненциально уменьшающуюся с глубиной, вдоль фронта волны. Эти две особенности закритической проходящей волны дают основание для ее специального наименования - она называется неоднородной плоской волной , в соответствии с характером распределения ее амплитуды по фронту.

Неоднородные плоские волны играют главенствующую роль в образовании преломленной (головной) волны, которую рассмотрим несколько позже в отдельном разделе. Здесь подчеркнем одно - все особенности неоднородной волны выявлены в результате анализа лишь волнового аргумента проходящей волны при закритическом падении плоской волны на границу раздела. Вид самой волновой функции этим анализом не затронут. Поэтому вернемся к исследованию поведения спектральных коэффициентов рассеивания и вторичных волн при закритическом падении первичной волны.

Итак, установлено, что при

где

.

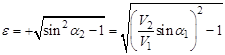Коэффициенты рассеивания А и В в этом случае описываются выражениями:

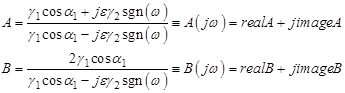
Знаком тождества подчеркнута комплексная зависимость коэффициентов рассеивания от частоты, оправдывающая введенное ранее определение А и В как спектральных коэффициентов рассеивания.