Поведение многих дискретных систем (таких как цифровые схемы с памятью или телекоммуникационные протоколы) можно описать моделью с конечным числом переходов, например, моделью конечного автомата. Конечный автомат сопоставляет последовательностям во входном алфавите последовательности в выходном алфавите. Для детерминированных автоматов методы построения проверяющих тестов достаточно хорошо развиты. Для недетерминированных автоматов, в которых одной входной последовательности может сопоставляться несколько выходных последовательностей, тесты активно развиваются, но в основном при тестировании используется предположение "о всех погодных условиях", т.е. предполагается, что есть возможность подавать входную последовательность, пока не пронаблюдаем все выходные реакции на нее. В данной работе изучается и улучшается метод построения тестов для недетерминированных автоматов относительно неразделимости для модели "черного ящика", предложенный в работе [1], в котором не используется ограничение "все погодные условия". Показывается, что избыточность тестов снижается, и при этом тест остается полным.

1. Основные определения и обозначения

1.1 Конечные автоматы и отношения между ними

Автоматом называется пятерка A = (S , I , O , h , s1), где S - множество состояний с выделенным начальным состоянием s1, I и O - соответственно входной и выходной алфавиты, h ÍS ´I ´S ´O - отношение переходов‑выходов. Элементами множества h являются четверки вида (s, i, s¢, o), называемые переходами ; при этом говорят, что автомат может перейти из состояния s ÎS под действием входного символа iÎI в состояние s¢ÎS с выдачей выходного символа oÎO, если четверка (s, i, s¢, o) содержится в h .

В случае, когда каждой паре вход-состояние соответствует не более одного перехода, автомат называется детерминированным , а в противном случае – недетерминированным (нд-автомат).

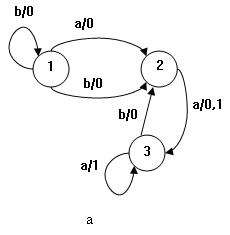
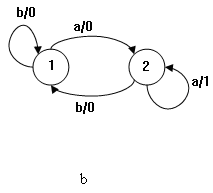
Рисунок 1 – Недетерминированный автомат A (а) и детерминированный автомат B (b)

Обозначим out (s , a) = {b:$s¢ÎS[(s, a, s¢, b) Îh]}, т. е. out (s , a) есть множество выходных реакций автомата в состоянии s на входную последовательность a.

Состояние s¢называется i -преемником состояния s, если существует такой выходной символ oÎO, что четверка (s, i, s¢, o) содержится в h . Множество состояний M ¢ÍS называется i -преемником множества состояний M ÍS , если M ¢есть множество всех i -преемников всех состояний множества M .

Если для любых (s, i, o) ÎS ´I´O в нд-автомате A существует не более одного перехода из состояния s под действием входного символа i с выходным символом o , то говорят, что нд-автомат A является наблюдаемым . Если для каждой пары (s, i) ÎS ´I существует хотя бы одна пара (s¢, o) ÎS ´O, такая что (s, i, s¢, o) Îh, то нд-автомат A называется полностью определенным . В противном случае автомат называется частично определенным или частичным .

Автомат A = (S ,I ,O ,h ,s ₁ ) называется инициальным , если в множестве состояний S выделено начальное состояние s ₁ .

Говорят, что состояние s ' достижимо из состояния s в автоматеA , если существует входная последовательность, которая переводит автоматA из состоянияs в состояниеs ' . Автомат называется связным , если любое его состояние достижимо из начального состояния[3].

Пусть A = (S , I , O , h , s1), B = (T , I , O , g , t1) – полностью определенные автоматы. Автомат B называется подавтоматом автомата A , если TÍS, t1 = s1 и gÍh. Пересечением автоматовA = (S , I , O , h , s ₁ )иB = (T , I , O , g , t ₁ )(обозначение A ÇB ), назовем максимальный связный подавтомат инициального автомата (S ´T , I , O , H , s1t1), в котором отношение переходов H определено следующим образом: (st , i , s ¢t ¢, o ) ÎH Û [(s , i , s ¢, o ) Îh Ù(t , i , t ¢, o ) Îg ]. Пересечение автоматов описывает общую часть поведения автоматов A и B и используется для построения входных последовательностей, различающих эти автоматы.

На рисунке 2 представлены автоматы A , B .

A	1	2	3	4
a	2/1 3/0	2/0	2/0 4/1	3/1
b	1/0	2/1	3/0	2/1

B	1	2	3	4
a	2/0 4/1	2/0	2/1 1/0	1/1
b	1/0	2/1	3/0	2/1

Рисунок 2 – Автоматы A , B

На рисунке 3 представлен автомат A ∩B .

AÇB	1,1	3,2	2,2	2,4
a	3,2/0 2,4/1	2,2/0	2,2/0	—
b	1,1/0	—	2,2/1	2,2/1

Рисунок 3 – Автомат A ÇB

--> ЧИТАТЬ ПОЛНОСТЬЮ <--