Для построенного таким образом P (если P ¹Æ) на соответствующем пути в дереве Tree_{S  T} будут перебраны все возможные подмножества P ¢ (P ¢ – это подмножество состояний S  T таких, что первый символ каждой пары из P ¢ содержится в P ). Значит, далее на данном пути в дереве Tree_{S  T} из рассмотрения можно исключить вершины, помеченные подмножествами К ¢, которые содержат подмножества P ¢– поэтому рассматриваемых вершин, помеченных подмножествами K , не содержащих подмножеств P , будет 2^{(| K |-| P |) × m} . Но также необходимо учесть все n вершин, помеченных подмножествами К , содержащими подмножества P , которые встретились на рассматриваемом пути в дереве Tree_S выше, чем l^й уровень, т.к. из данных вершин подмножества P исключать не можем. Следовательно, количество вершин, помеченных подмножествами K , для усечения дерева в таком случае составляет 2^{(| K |-| P |) × m} +n вершин.

2. Далее рассмотрим случай, когда s ₀ ÎK , но s ₀ не принадлежит множеству P . По алгоритму 1 для случая s ₀ ÎK вершина, помеченная подмножеством K , объявляется листом, если путь из корня в данную вершину содержит (2^{| K | × m -1} +1) вершин, помеченных подмножествами множества K . Если же на данном пути для каждого P_i ÎP встретилось, как и в предыдущем случае, необходимое число вершин, помеченных подмножествами P_i , то листовой будет являться вершина, путь из корня в которую содержит 2^{(| K |-| P |) × m -1} +n +1 вершин, помеченных подмножествами K .

3. Если s ₀ ÎK и s ₀ ÎP , т.е.s ₀ принадлежит одному из подмножеств P_j ÎP , то необходимо, чтобы на рассматриваемом пути дерева встретилось (2^{| Pj | × m -1} ) вершин, помеченных подмножествами P_j , если P_j добавляется к P на шаге 2 построения множества P , либо (2^{(| Pj |-| Q |) × m -1} ) вершин – если на шаге 3. Для остальных подмножеств P_i из P требуется встретить такое же количество вершин, как и в случае 1.Тогда можно исключить подмножества P из вершин, помеченных подмножествами K начиная с l^го уровня, и вершина, помеченная подмножеством K , объявляется листом, если путь из корня в данную вершину содержит 2^{(| K |-| P |) × m} +n вершин, помеченных подмножествами множества K .

4. Если для данного пути дерева P = Æ, то |P | = 0, n = 0 и пользуемся алгоритмом 2.

На рисунке 9 представлено усеченное дерево преемников для спецификации, изображенной на рис. 5, построенное согласно алгоритму 3. Суммарная длина полного проверяющего теста в этом случае составляет 200 символов, что на 77 символов меньше, чем для алгоритма 2.

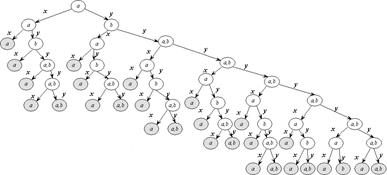
Рисунок 9 – Усеченное дерево преемников, построенное по алгоритму 3

ЗАКЛЮЧЕНИЕ

В данной работе изучен метод построения тестов для недетерминированных автоматов относительно модели "черного ящика", предложенный в работе [1]. Этот метод, в отличие от других методов синтеза тестов для недетерминированных автоматов, не ориентирован на выполнение предположения "о всех погодных условиях". Исследованы возможные подходы к улучшению рассмотренного метода и предложена модификация данного метода. Показано, что тест, построенный согласно модифицированному методу, будет по-прежнему полным, но при этом менее избыточным.

ЛИТЕРАТУРА

1. Natalia Shabaldina, Khaled El-Fakih, Nina Yevtushenko. Testing Nondeterministic Finite State Machines With Respect to the Separability Relation. Lecture Notes in Computer Science, 2007(4581), pp. 305-318.

2. Шабалдина Н.В., Евтушенко Н.В. Построение тестов для конечных автоматов относительно неразделимости . Вестник ТГУ. Приложение. Серия "Математика. Кибернетика. Информатика". 2007. № 23. С. 287– 290.

3. Евтушенко Н.В., Петренко А.Ф., Ветрова М.В. Недетерминированные автоматы: анализ и синтез. Ч. 1. Отношения и операции. – Томск: Томский государственный университет, 2006. – 142 с.

4. Евтушенко Н.В., Спицина Н.В. О верхней оценке длины разделяющей последовательности