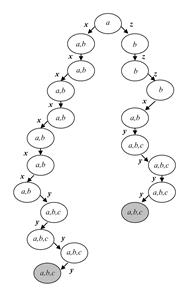
Рисунок 6 – Усеченное дерево преемников, построенное по алгоритму 2

3. Улучшение метода построения полного проверяющего теста относительно модели неисправности <S , (£,≁), Â _m >

3.1 Исследование условий усечения дерева

Алгоритм 2 не доставляет кратчайшего теста. Для иллюстрации этого факта рассмотрим тестовую последовательность xyyyyyyy из предыдущего примера, которой в усеченном дереве преемников (рис. 6) соответствует путь a_x a_y b_y {a ,b }_y {a ,b }_y {a ,b }_y {a ,b }_y {a ,b }_y {a ,b }. Прямым перебором можно убедиться, что если автомат-реализация имеет состояния 1 и 2, тогда соответствующий путь в усеченном дереве Tree_{S Ç T} , построенном по пересечению эталонного автомата и реализации, будет уже усечен после {a 1}_x {a 2}_y {b 1,b 2}_y {b 1}_y {b 2}_y {a ,b }, т.к. для подмножества а были перебраны все варианты и из последующих подмножеств его можно исключить. Таким образом, при уточнении условий усечения дерева данную тестовую последовательность можно сократить на 3 символа.

Сократить тестовую последовательность можно также и в более общем случае, когда на рассматриваемом пути дерева перебраны все возможные варианты для состояний некоторого множества P , являющегося подмножеством множества K . Рассмотрим эталонный автомат S , изображенный на рисунке 7, и m =2.

S	a	b	c
x	a/0 b/1	a,b/1	a/1
y	a,b/0	c/1	b/1 c/0
z	b/1	b/0	a/0

Рисунок 7 - Автомат S

Для подмножества состояний {a , b , c } для усечения дерева по алгоритму 2 необходимо, чтобы путь из корня дерева в листовую вершину покрывал 2^{3 m -1} +1=33 вершины, помеченные подмножествами этого множества. Однако, т.к. на левом пути дерева, представленного на рисунке 8, сначала встречается 8 вершин, помеченных подмножествами {a , b }, а именно такое число вариантов обеспечивает перебор всех подмножеств {a 1, a 2, b 1, b2} в дереве Tree_{S Ç T} , то далее на данном пути подмножество {a , b } из рассмотрения исключается. Таким образом, соответствующий путь в дереве Tree_{S Ç T} будет усечен после {a 1}_x {a 2,b 1,b 2}_x {a 2,b 1}_x {a 2,b 2}_x {a 2}_x {b 1}_x {b 2}_x {b 1,b 2}_y {c 1,c 2}_y {c 1}_y {c 2}_y {a ,b ,c }, и длина тестовой последовательности составляет всего 11 символов.

Рисунок 8 – Часть усеченного дерева преемников

Естественно, сокращение тестовой последовательности можно также обобщить и для случая, когда на рассматриваемом пути дерева перебираются все подмножества для нескольких подмножеств P_i множества K , в том числе и в случае, когда эти подмножества пересекаются. Данный случай иллюстрирует правый путь дерева, изображенного на рисунке 8. На этом пути дерева сначала перебираются все возможные подмножества для P ₁ ={b }. Для пересекающегося с P ₁ множества P ₂ ={a ,b } теперь достаточно всего трех вершин, помеченных подмножествами P ₂ , чтобы были перебраны все возможные подмножества P ₂ . И соответствующий путь в дереве Tree_{S Ç T} усекаетсяпосле {a 1}_z {b 1,b 2}_z {b 1}_z {b 2}_x {a 2}_y {c 1,c 2}_y {c 1}_y {c 2}_y {a ,b ,c }, а длина тестовой последовательности составляет 8 символов.

Таким образом, можно модифицировать метод построения полного проверяющего теста относительно модели неисправности <S , (£,≁), Â _m > (алгоритм 2), уточнив условия усечения дерева преемников.

3.2 Модифицированный метод построения полного проверяющего теста относительно модели неисправности <S , (£,≁), Â _m >

Алгоритм 3. Построение полного проверяющего теста относительно модели неисправности <S , (£,≁), _m >

Вход: Полностью определенный автомат S и верхняя граница m числа состояний любой реализации S

Выход: Полный проверяющий тест TS относительно модели неисправности <S , (£,≁), _m >

Шаг 1. Построим усеченное дерево преемников автомата спецификации S . Корнем дерева на нулевом уровне является начальное состояние s 0 автомата S ; вершины дерева помечены подмножествами состояний автомата S . Пусть уже построены j уровней дерева, j ³ 0. Для заданной нетерминальной вершины j ^го уровня, помеченной подмножеством состояний К , и для заданного входного символа i , в дереве есть ребра, помеченные символом i , в вершину, помеченную i -преемниками подмножества К . Текущая вершина Current на k ^м уровне, k > 0, помеченная подмножеством К состояний из множества S , объявляется листом дерева, если путь из корня в вершину Current содержит:

· 2^{(| K |-| P |) × m} +n вершин, помеченных подмножествами множества К , если s ₀ ÏK или s ₀ ÎK и s ₀ ÎP ;

· 2^{(| K |-| P |) × m -1} +n + 1вершин, помеченных подмножествами множества К , если s ₀ ÎK и s ₀ ÏP ;

где P – это такое подмножество состояний из множества K , что до некоторого l ^го уровня (l < k ) перебраны все возможные подмножества P , а n – это количество вершин на данном пути, помеченных подмножествами К , содержащими подмножества P , которые находятся на уровнях не ниже l ^го уровня дерева (если P = Æ, то n = 0). Множество P строится итеративно:

1. P = Æ;

2. P = P ÈP_i для каждого подмножества P_i множества K , для которого путь из корня в вершину Current содержит (2^{| P i | × m} -1) вершин, помеченных подмножествами P_i (или (2^{| P i | × m -1} ) вершин в случае s 0ÎP_i );

3. P= PÈP_j для всех существующих пар P_i ÎP и P_j ÏP (P_j ÌK ) таких, что P_i ÇP_j = Q и путь из корня в вершину Current содержит (2^{(| Pj |-| Q |) × m} -1) вершин, помеченных подмножествами P_j , если s 0ÏP_j или s 0ÎQ , либо (2^{(| Pj |-| Q |) × m -1} ) вершин в случае s 0ÎP_j .

Шаг 2. Включаем в TS каждую входную последовательность, которая помечает путь из корня к листу в усеченном дереве.

Теорема 2.

Для заданного эталонного автомата S и целого числа m алгоритм 3 доставляет полный проверяющий тест относительно модели неисправности <S , (£,≁), _m >.

Доказательство.

1. Рассмотрим самый общий случай – подмножество K состояний из множества S , и начальное состояние s ₀ ÏK . Согласно алгоритму 1, вершина усеченного дерева преемников Tree_S , помеченная подмножеством K , объявляется листом дерева, если путь из корня в эту вершину содержит 2^{| K | × m} вершин, помеченных подмножествами множества К . Это соответствует перебору всех возможных подмножеств К ¢в усеченном дереве приемников Tree_{S  T} , построенному по пересечению эталонного автомата S и некоторой реализации T , где К ¢ – это подмножество состояний пересечения S  T таких, что первый символ каждой пары из К ¢ содержится в К .

Предположим, что существует такое подмножество состояний P из множества K , что до некоторого l ^го уровня дерева на пути из корня в вершину Current перебраны все возможные подмножества P . Множество P строится итеративно следующим образом:

Шаг 1. P = Æ.

Шаг 2. P = P ÈP_i для каждого подмножества P_i множества K , для которого путь из корня в вершину Current содержит (2^{| P i | × m} -1) вершин, помеченных подмножествами P_i . Добавление каждого такого P_i в множество P справедливо, т.к. если путь содержит указанное количество повторов, то этим перебираются все возможные варианты подмножеств P_i .