Курсовая работа: Нарисна геометрія

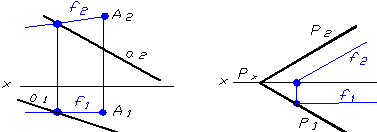
а) б)

Рисунок 1.24 – Побудова фронталі площини

Профільними прямими називають прямі, які належать площині та паралельні профільній площині проекцій.

Лініями найбільшого нахилу до площини проекцій називають прямі, які належать заданій площині та паралельні горизонталі, фронталі або профільній прямій. Лінії найбільшого нахилу до площин проекцій дають можливість визначати кути нахилу до відповідних площин проекцій.

4. Перетворення комплексного креслення

Аналізуючи положення прямих та площин стосовно площин проекцій зрозуміло що, лише у тому випадку, коли вони займають особливе положення (рисунки 1.8, 1.10, 1.20), на одній (або двох) площині проекцій матимемо натуральну величину. Якщо прямі чи площини займають загальне положення, натуральної величини бути не може. Для визначення натуральної величини розмірів площини чи відрізка існує кілька способів: заміна площин проекцій, обертання навколо проеціювальної осі, обертання навколо прямої рівня, плоскопаралельне переміщення.

Щоб визначити натуральну величину геометричного об’єкта, необхідно або змінити систему площин проекцій так, щоб об’єкт зайняв особливе положення, або розвернути сам об’єкт у просторі так, щоб він зайняв особливе положення стосовно існуючої системи площин проекцій.

4.1 Спосіб заміни площин проекцій

Суть способу полягає в тому, що положення геометричного об’єкта у просторі залишається незмінним, а одну з площин проекцій замінюють новою, яка створює з другою площиною проекцій нову систему взаємно перпендикулярних площин, відносно якої геометричний об’єкт займе особливе положення. Замін може бути декілька. Способом заміни площин можна розв’язувати багато позиційних та метричних задач нарисної геометрії.

Приклад 2 Визначити натуральну величину відрізка АВ.

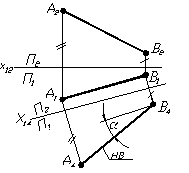
Рисунок 1.25 – Визначення натуральної величини відрізка способом заміни площин проекцій

Для визначення натуральної величини відрізка необхідно ввести допоміжну площину проекцій П₄ , яка перпендикулярна до горизонтальної площини проекцій та паралельна відрізку АВ.

Площина П₄ вводиться на будь – якій відстані від відрізка АВ. На комплексному кресленні достатньо провести нову вісь Х₁₄ паралельно горизонтальній проекції відрізка АВ та з А₁ та В₁ провести лінії зв’язку, перпендикулярні до осі Х_14, на яких відкласти віддалення від горизонтальної площини проекцій, які вимірюються на площині П₂ (зроблені позначки однією та двома рисками). На рисунку 1.25 позначений кут нахилу (a) прямої АВ до горизонтальної площини проекцій – це буде кут між НВ прямої АВ та прямою паралельною осі Х₁₄ .

Щоб визначити кут нахилу прямої АВ до фронтальної площини проекцій, необхідно ввести площину, перпендикулярну до площини П₂ та паралельну відрізку АВ.

Приклад 3 Визначити натуральну величину трикутника АВС (рис. 1.26).

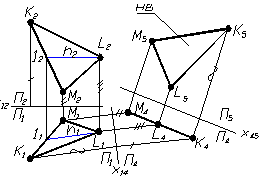
Рисунок 1.26 – Визначення натуральної величини трикутника способом заміни площин проекцій

Для розв’язання задачі двічі виконують заміну площин проекцій.

Перша заміна виконана таким чином, щоб трикутник перетворити у проеціювальну площину. Для цього необхідно нову вісь Х₁₄ провести перпендикулярно до горизонтальної проекції горизонталі (h₁ ) – це ознака того, що трикутник перпендикулярний до нової площини проекцій (П₄ ), на яку він проектується у відрізок.

Друга заміна виконана таким чином, щоб трикутник перетворити у площину рівня. Для досягнення цього необхідно нову вісь Х₄₅ провести паралельно відрізку, в який спроектувався трикутник АВС.

Відстані, які необхідно виміряти та відкласти від нових осей, позначені відповідними лініями.

4.2 Спосіб обертання навколо проеціювальної осі

Суть способу полягає в тому, що система площин проекцій залишається незмінною, а геометричний елемент змінює своє положення у просторі, займаючи особливе положення відносно площин проекцій. Усі точки геометричного об’єкта обертаються у площинах, паралельних тій площині проекцій, відносно якої вісь обертання перпендикулярна. Якщо вісь обертання перпендикулярна до горизонтальної площини проекцій, то на комплексному кресленні всі горизонтальні проекції точок геометричного об’єкта пересуваються по

колах, а фронтальні проекції – по прямих, паралельних осі Х.

Приклад 4 Визначити натуральну величину трикутника АВС (рис. 1.27).

Рисунок 1.27 – Визначення натуральної величини трикутника способом обертання навколо проеціювальної осі

Для визначення натуральної величини трикутника АВС необхідно провести горизонталь площини.