Курсовая работа: Нарисна геометрія
Друге обертання виконано навколо прямої, проведеної через точку В, перпендикулярно до площини П2 . Трикутник переведений у положення паралельності площині П1 , тому горизонтальна проекція трикутника – це його натуральна величина.
Основним недоліком способу обертання навколо проеціювальної осі є накладання одного зображення на інше. При розв’язанні задач способом плоскопаралельного переміщення цього недоліку немає.
4.3 Спосіб плоскопаралельного перенесення
Суть способу полягає в тому, що система площин залишається незмінною, а геометричний об’єкт займає особливе положення відносно площин проекцій, що дає можливість розв’язувати позиційні та метричні задачі. Цей спосіб вважають винятковим способом обертання навколо проеціювальної осі. На комплексному кресленні одна з проекцій геометричного об’єкта, не змінюючи своїх розмірів, змінює своє положення відносно осі Х12 . Тоді всі точки другої проекції пересуваються по прямих, паралельних осі Х12 .
Приклад 5 Визначити натуральну величину відрізка АВ.
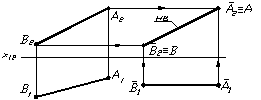
Рисунок 1.28 – Визначення натуральної величини відрізка способом плоско паралельного переміщення
У даному прикладі для визначення натуральної величини відрізка способом плоскопаралельного переміщення горизонтальну проекцію відрізка (А1 В1 ) розміщують на вільному місці креслення паралельно осі Х12 . Фронтальна проекція відрізка АВ буде його натуральною величиною. Для її побудови необхідно з фронтальних проекцій точок А2 та В2 провести лінії, паралельні осі Х12 до перетину з лініями проекційного зв’язку, проведених від горизонтальних проекцій цих точок.
Приклад 6 Визначити натуральну величину трикутника АВС.
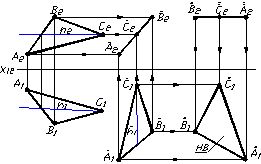
Рисунок 1.29 – Визначення натуральної величини трикутника способом плоскопаралельного переміщення
Щоб визначити натуральну величину трикутника АВС, необхідно спочатку перетворити площину загального положення в площину проеціювальну (у наведеному прикладі – фронтально – проеціювальну), а потім у площину рівня (на рисунку 1.29 – це площина горизонтального рівня). Для виконання таких перетворень перш за все необхідно провести горизонталь площини трикутника.
Щоб перетворити площину загального положення у площину фронтально проеціювальну, необхідно горизонтальну проекцію трикутника розмістити так, щоб горизонталь його стала перпендикулярна до осі Х. У цьому разі всі фронтальні проекції вершин трикутника будуть пересуватися паралельно осі Х до перетину з лініями зв’язку, проведеними з горизонтальних проекцій вершин трикутника АВС. На фронтальну площину проекцій трикутник проектується у вигляді відрізка прямої лінії.
Щоб перетворити площину фронтально-проеціювальну у площину горизонтального рівня, необхідно фронтальну проекцію трикутника (відрізок прямої) розмістити паралельно осі Х – тоді горизонтальні проекції вершин трикутника будуть пересуватися паралельно осі Х до перетину з відповідними лініями зв’язку. Горизонтальна проекція трикутника – це натуральна величина його.
5. Поверхні
Світ поверхонь багатогранний та різноманітний. Із усього різноманіття найбільш поширеними є багатогранники та поверхні обертання.
Багатогранниками називають поверхні, які обмежені площинами (гранями). До багатогранників відносять призми та піраміди (рис. 1.30).
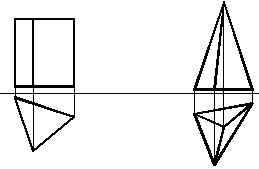
Рисунок 1.30 – Багатогранники
Залежно від того, яка геометрична фігура є основою багатогранника, їх називають тригранними, чотиригранними, п’ятигранними призмами чи пірамідами.
Поверхні обертання утворені обертанням твірної (прямої або кривої лінії) навколо нерухомої осі. До поверхонь обертання відносять конус, циліндр, сферу, тор. На рисунку 1.31 наведені комплексні креслення конуса, циліндра, сфери та тора.
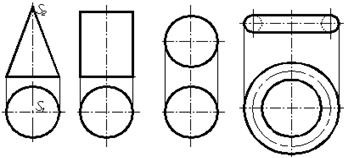
Рисунок 1.31 – Поверхні обертання
5.1 Точки на поверхнях
Для побудови проекції точки, яка належить поверхні, за заданою проекцією необхідно перш за все з’ясувати, якому елементу поверхні точка належить.
Якщо точка належить поверхні призми чи піраміди, то для побудови другої проекції точки достатньо провести лінії проекційного зв’язку. При побудові проекцій точок, які належать будь-якій поверхні, необхідно пам’ятати про видимість. Невидимі проекції точок позначають у дужках, наприклад, (А1 ) – горизонтальна проекція точки А невидима.
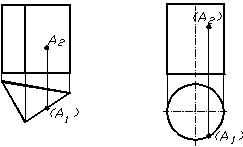
Рисунок 1.32 – Точки на поверхнях
На рисунку 1.32 наведені приклади побудови горизонтальних проекцій точок, які належать поверхням піраміди та циліндра. Задані фронтальні проекції точок. Для побудови горизонтальних проекцій точок необхідно провести лінії зв’язку на відповідні елементи поверхонь з урахуванням видимості. У наведених прикладах для поверхні призми фронтальна проекція точки А видна, її горизонтальна проекція – невидна. На поверхні циліндра – фронтальна та горизонтальні проекції точки А не видні.
Для визначення точок, які належать поверхням піраміди або конуса, необхідно виконати допоміжні побудови.