Курсовая работа: Нарисна геометрія
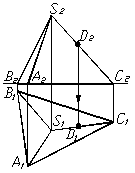
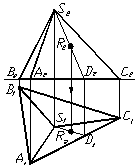
а) б)
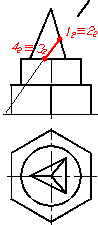
Рисунок 1.33 – Точки на поверхні піраміди
Якщо точка належить грані піраміди, то через задану точку у відповідній грані необхідно провести допоміжну пряму.
У наведеному прикладі задана фронтальна проекція точки R. Точка R належить грані SAC. Для побудови її горизонтальної проекції послідовно виконують такі дії:
- через задану точку на грані SAC провести фронтальну проекцію допоміжної прямої SD;
- побудувати горизонтальну проекцію допоміжної прямої (S1 D1 );
- по лінії проеційного зв’язку визначити горизонтальну проекцію точки R на грані ASC.
5.2 Перетин поверхонь проеціювальними площинами
Якщо будь-яку геометричну поверхню перетнути проеціювальною площиною, то одна з проекцій лінії перетину очевидна – це відрізок прямої лінії, який збігається з проекцією проеціювальної площини. Другу проекцію лінії перетину будують за точками, які їй належать.
Якщо проеціювальна площина перетинає поверхню призми або циліндра, ніякі побудови не виконуються, а лише позначаються проекції лінії перетину. На рисунку 1.34 наведені приклади побудови проекцій лінії перетину призми та циліндра фронтально-проеціювальними площинами та визначена натуральна величина перерізів способом заміни площин проекцій (для призми) та способом плоскопаралельного переміщення (для циліндра).
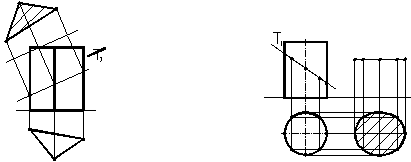
а) б)
Рисунок 1.34 – Перетин призми та циліндра фронтально-проеціювальними площинами
Горизонтальна проекція фігури перерізу піраміди фронтально-проеціювальною площиною наведена на рисунку 1.35 Для її побудови проведені лінії проеційного зв’язку на відповідні ребра піраміди. Натуральна величина фігури перетину визначена способом плоскопаралельного переміщення.
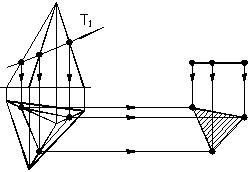
Рисунок 1.35 – Перетин піраміди фронтально-проеціювальною площиною
Фігура перерізу конуса фронтально-проеціювальною площиною залежить від положення січної площини відносно елементів конуса. На рисунку 1.36 наведені приклади побудови перерізів конуса фронтально-проеціювальними площинами.
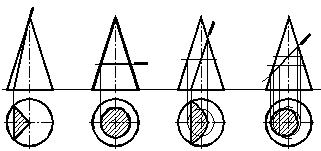
Рисунок 1.36 – Переріз конуса проеціювальними площинами
При виконанні контурів машинобудівних креслень можливі варіанти, коли необхідно побудувати перетин складного тіла проеціювальною площиною (рис. 1.37а) та визначити натуральну величину перерізу. Пропоноване на рисунку 1.37а тіло складається із послідовно встановлених одну на одну шестигранної призми, циліндра та тригранної піраміди.
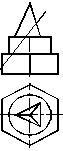
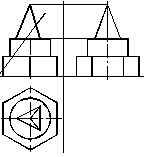
а) б)
Рисунок 1.37 – Переріз складного тіла фронтально-проеціювальною площиною
Для розв’язання цієї задачі необхідно перш за все побудувати профільну проекцію пропонованого тіла (рис. 1.37б) – вигляд зліва.
Переріз піраміди фронтально-проеціювальною площиною – чотирикутник 1234. Фронтальна проекція його – це відрізок, обмежений точками 12 ≡22 та 32 ≡42 , який визначається без зайвих побудов. Горизонтальну та профільну проекції чотирикутника одержують по лініях проеційного зв’язку, визначаючи точки на відповідних елементах піраміди: точки 1 та 2 належать ребрам, а 3 та 4 – основі піраміди. На рисунку 1.38а, б та в наведена поетапна побудова фігури перерізу піраміди заданою площиною.
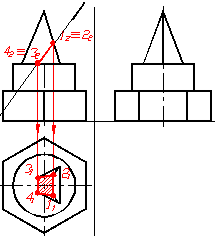
а) б)