Курсовая работа: Обработка данных методом преломленных волн

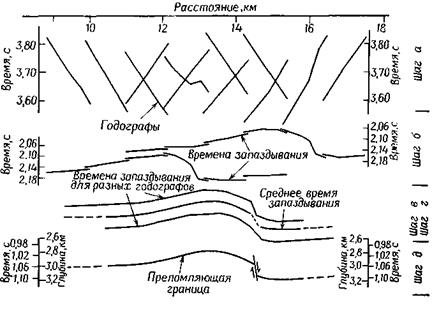
Рис. 4. Интерпретация встречных профилей по методу времен запаздывания.

неточным выбором значения V ₂ ; следовательно, значение V ₂ необходимо исправить и повторить этапы (б), (в), пока кривые не станут параллельны (на практике уточнение V ₂ обычно производится только один раз);

д) разделение полных времен запаздывания на относящиеся к пунктам взрыва и пунктам приема (при этом последние относят к проекциям на поверхность точек, в которых сейсмическая волна падает на преломляющую границу и отходит от нее, т. е. к точкам S и Т на рис. 3); масштаб времен, если требуется, можно перевести в масштаб глубин с помощью формулы (4).

в) Метод Тарранта. В этом методе времена запаздывания используются для определения положения точки Q (рис. 5, а ), в которой энергия, регистрируемая в пункте R , отходит от границы. Обозначив d_g время запаздывания, связанное с траекторией QR , запишем

,

Откуда

. (6)

Мы получили уравнение эллипса в полярной системе координат. Эллипс —это геометрическое место таких точек Q (рис. 5, б ),

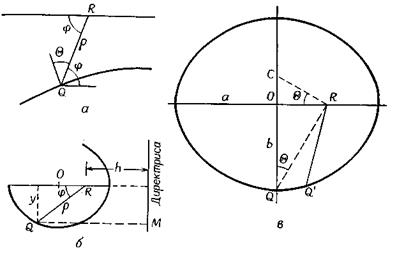Рис. 5. Интерпретация по методу Тарранта а — связь между точкой приема К и точкой Q отхода от границы; б —схема, поясняющая, что геометрическим местом точек Q является эллипс, в одном из фокусов которого располагается точка R ; в — геометрия эллипса, проходящего через точку Q .

для которых отношение QR / QM остается постоянным (равным эксцентриситету e, который для эллипса меньше 1, т. е.

r/(h + rcosj) = e,

а следовательно,

r = eh /(1 - ecosj). (7)

Большая ось эллипса 2а = r_{j =0} + r_{j = p} = 2 eh / (1—e² ). Малую полуось b можно найти, записав y = rsinjи определив у _max ,; это дает b = eh ( 1— e² )^-1/2 . Расстояние от фокуса R до центра эллипса О равно

r|_{j =0} — а = eh /(1 — e) —eh /(1 — e² ) = ea .

Если принять e = sinQ и h = V ₂ d_g , выражение (7) перейдет в (6).

Для горизонтальной преломляющей границы получается эллипс (рис. 5, в ) с а = V ₂ d_g tgQsecQ, b = V ₂ d_g tgQи OR = V ₂ d_g tg² Q. Подобным же образом RQ = b / cos Q = а и ÐOQR = arctg(ОR / b ) = Q, OQ = OR ctgQ = V ₂ d_g tgQ.

В окрестности Q эллипс можно аппроксимировать окружностью того же радиуса кривизны. Если записать уравнение эллипса в декартовой системе координат

(x / a )² +(y / b )² = 1,

то радиус кривизны r можно выразить как

r = (1+y ’ ² )^3/2 /y ’’ ,

где у' = — ( b /а)² (х + у) и у" = —( b /а)² (у — ху')/у² ; в точке Q у' = 0 и у" = b /а² . Следовательно,

r = a ² lb = V ₂ d_g /cos³ Q = V ₂ d_g tgQsec² Q

и центр кривизны С лежит в точке (0, r — b ) , т. е. (0,V ₂ d_g tg³ Q). Следовательно, ÐCRO = arctg( CO / RO ) = Q, а значит, Ð CRQ — прямой угол.

Чтобы применить описанный метод, мы должны определить скорости V ₁ и V ₂ и время запаздывания в пункте взрыва d_S , а затем рассчитать d_g по формуле

d_g = t_R — x / V ₂ — d_S .

После этого можно вычислить OR , OQ и затем найти положение С, проведя перпендикуляр RC к RQ . Из С проводим дугу окружности, соответствующую преломляющей границе в окрестности точки Q . Если наклон границы отличен от нуля, точкой выхода станет Q ' и длина дуги QQ ' увеличивается при росте угла наклона границы. Но даже для углов падения умеренной величины дуга эллипса QQ ' будет близка к дуге окружности, проходящей через Q , и, таким образом, огибающая дуг окружностей достаточно точно отобразит преломляющую границу.

Метод Тарранта удобен, когда наклон границ умеренный или даже большой, а преломляющая граница криволинейна или имеет неправильную форму. Принципиальным ограничением является точность определения V ₂ .