Курсовая работа: Обработка опытных данных методом МНК

Y=ax³ +bx² +cх+d

Также за эмпирическую формулу можно взять любой полином Y = P_n (x), обратную степенную функцию Y=1/Q_n (x) или логарифмическую Y = aln(bx) + c.

Ниже приведены наиболее употребимые формулы и соответствующие им графики.

3.1. Степенная зависимость (геометрическая регрессия)

Степенная зависимость имеет вид

(3)

Во всех случаях при При в точке кривая касается оси абсцисс. В этом случае, чем больше , тем ближе подходит кривая к оси абсцисс при и тем быстрее она возрастает при

При в точке кривая касается оси ординат. При кривая ближе подходит к оси ординат, чем к оси абсцисс, при наоборот.

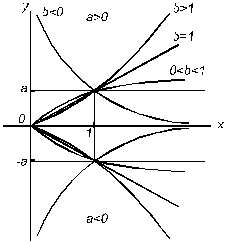
Рисунок 1

График степенной зависимости

Покажем, как нахождение приближающей функции в виде геометрической регрессии может быть сведено к нахождению параметров линейной функции. Предполагая, что в исходной таблице 1 значения аргумента и функции положительны, прологарифмируем равенство (3) при условии

(4)

Введем новую переменную тогда будет функцией от t . Обозначим тогда равенство (4) примет вид:

т.е. задача свелась к отысканию приближающей функции в виде линейной.

Практически для нахождения приближающей функции в виде степенной (при сделанных выше предположениях) необходимо проделать следующие операции:

1) по данной таблице 1 составить новую таблицу 2, прологарифмировав

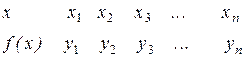Таблица 1 Таблица 2

2) по новой таблице 2 найти параметры и приближающей функции вида

3) используя примененные обозначения, найти значения параметров и и подставить их в выражение (3).

Окончательно получаем:

(5)

3.2. Показательная зависимость

Показательная зависимость имеет вид

(6)

Во всех случаях при . Если то при кривая растет с увеличением тем быстрее, чем больше При она приближается к оси абсцисс с возрастанием тем быстрее, чем больше абсолютная величина

Если найденная на опыте зависимость от является показательной, то график зависимости от представляет собой прямую линию, тангенс угла наклона которой равен параметру Если значение при неизвестно, то величину параметра можно найти по формуле для ряда значений а затем взять среднее.

Рисунок 2 График показательной функции

Найдем коэффициенты и для исходной таблицы 1, если известно, что приближающую функцию целесообразно искать в виде показательной функции (6).

Прологарифмируем равенство (6) :

(7)

приняв обозначения перепишем (7) в виде: