Курсовая работа: Обработка опытных данных методом МНК

Таким образом приближающая показательная функция нехитрыми преобразованиями сведена к линейной, следовательно, для определения коэффициентов и показательной функции можно воспользоваться выведенной для линейной функции формулой

(9)

Итак, для нахождения приближающей функции в виде (6) нужно прологарифмировать значения функции в исходной таблице 1 и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы 3 приближающую функцию вида (8).

Таблица 1 Таблица 3

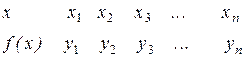Окончательно получаем:

(9)

Рисунок 3 – График логарифмической функции

Замечание: формулам

(10)

(11)

соответствуют кривые, изображенные на рисунках 1 и 2, сдвинутые вверх или вниз на величину . Например, кривая, изображенная на рисунке 3, соответствует формуле при и Чтобы найти параметры этих формул, следует сначала определить значение Иногда величину можно легко найти по значению, к которому стремится при возрастании (при ) или по значению при (для формулы 10 при ). Можно также воспользоваться формулой

где и — ординаты произвольных (но достаточно далеких) точек с абсциссами ,, а ордината соответствует абсциссе в случае формулы (10) и абсциссе в случае формулы (11).

3.3. Логарифмическая функция

Будем искать приближающую функцию в виде

(12)

Для перехода к линейной функции достаточно выполнить подстановку

Отсюда следует, что для нахождения значений a и b нужно прологарифмировать значения аргумента в исходной таблице 1 и для новой таблицы 4 найти приближающую функцию в виде линейной y= at+ b. Коэффициенты a и b найденной функции подставить в формулу 2.14.

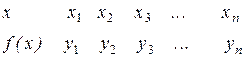Таблица 4

Таблица 5

Окончательно получим:

(13)

Рисунок 4 График логарифмической функции

4. Метод наименьших квадратов

Запишем сумму квадратов отклонений для всех точек х₀ , х_1, …,х_m

(3)

Параметры а₀ , а_1, …,а_m эмпирической формулы будем находить из условия минимума функции S= S(а₀ , а_1, …,а_m ). В этом состоит метод наименьших квадратов.

В теории вероятностей доказывается, что полученные таким методом значения параметров наиболее вероятны.

Поскольку здесь параметры а₀ , а_1, …,а_m выступают в роли независимых переменных функции S, то ее минимум найдем, приравнивая нулю частные производные по этим переменным:

(4)

Полученные соотношения – система уравнений для определения параметров а₀ , а_1, …,а_m

Рассмотрим применение метода наименьших квадратов для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим многочлен: