Курсовая работа: Обработка опытных данных методом МНК

Формула (9) для определения суммы квадратов отклонений S примет вид

(6)

Для составления уравнений (4) найдем частные производные функции S= S(а₀ , а_1, …,а_m ):

Приравнивая эти выражения нулю в соответствии с уравнениями (4) и собирая коэффициенты при неизвестных а₀ , а_1, …,а_m получаем следующую систему уравнений:

………………………………………….

Решая эту систему линейных уравнений, получаем коэффициенты

а₀ , а_1, …,а_m многочлена (5), которые являются искомыми параметрами эмпирической формулы.

5. БЛОК-СХЕМА решения задач

6 .Решение задачи в MathCAD

Для решения поставленной задачи необходимо подобрать эмпирическую формулу такую, которая наилучшим образом отражала бы заданное экспериментальное распределение точек (таблица исходных данных). Для этого воспользуемся графическими возможностями программы MathCad.

На рис.4 представлено точечное распределение экспериментальных данных, задания курсовой работы.

Рисунок 4 – Распределение точек

С помощью программы Mathcadподберем функцию, максимально близко проходящую к данным точкам, либо проходящую через них. Т.е. определим функциональную зависимость yот х. Для этого воспользуемся методом перебора возможных вариантов: сначала оценим погрешность аппроксимации линейной, степенной и логарифмической функций. Оптимальной будем считать ту аппроксимирующую функцию, которая позволяет достичь минимального среднеквадратического отклонения

Рассмотрим линейную функцию

Для того, чтобы провести график данной функции и оценить погрешность аппроксимации, необходимо найти коэффициенты aи b. Воспользуемся встроенными

Аппроксимация прямой

аппроксимирующая функция

Рисунок 5 – Линейная функция

Среднеквадратическое отклонение функции :

Таким образом, среднеквадратическое отклонение значений функции от значений распределения полученных данных достаточно велико, следовательно, данная функция не является оптимальной

Рассмотрим теперь аппроксимацию полиномом. Степень полинома не может превышать 9, т.к. всего точек в распределении данных - 10. Будем изменять значение параметра n - степени полинома, выберем два разных полинома со степенями, например 2 и 3 и сравним погрешность такой аппроксимации

степень полинома

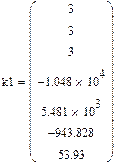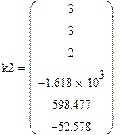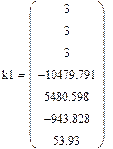Результаты аппроксимации данных полученными полиномами polyи poly2 представлены на рис. 6

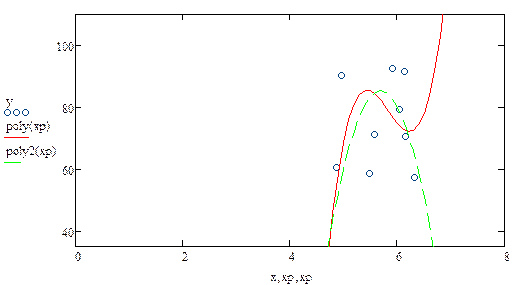Рисунок 6– График степенной функции

Оценим погрешность данного способа аппроксимации для функции F(x) = -10479.791+ 5480.598*x -( -943.828)*x² + 53.93*x³ :

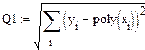Для функции F(x) = -1617.748+ 598.477*x– (-52.578)*x² :

Рассмотрим логарифмическую функцию.

Будем располагать точки на различных графиках

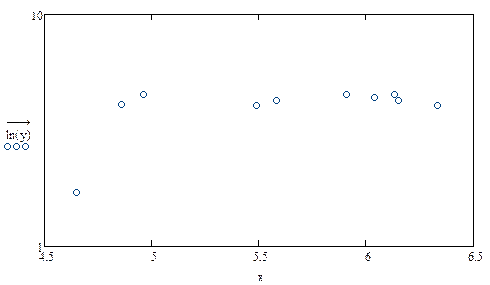Рисунок 7 – Экспериментальные данные в полулогарифмической шкале (lnу)

Рисунок 8 - Экспериментальные данные в полулогарифмической шкале (lnx)

Рисунок 9 – Логарифмические шкалы по обеим осям

Можно заметить что на рисунке 7 точки приближенно укладываются в прямую линию. Это означает что подбираемую функцию можно линеаризовать, если заменить вектор у на ln(у).

В уравнении ln(у) = а*х + ln(b) заменим ln(у) на у1, а заменим на а0, ln(b) y на b0.

Применили линейную аппроксимацию для расчета коэффициентов а и ln(b), а затем А и В.