Коммуникации и связь / Курсовая работа: Одновісний гіроскопічний стабілізатор

Курсовая работа: Одновісний гіроскопічний стабілізатор

Побудуємо АФЧХ (рис.)

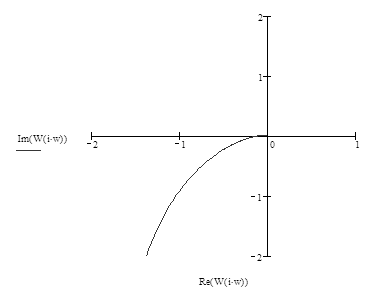
Рис.3.3.1

За критерієм Найквіста, якщо характеристичне рівняння розімкненої САК не має правих коренів, то замкнена САК буде стійкою, коли АФЧХ розімкненої САК не охоплює точку з координатами ().

Оскільки розімкнена САК, що досліджується, має праві корені і не охоплю точку з координатами () (рис. 3.3.1), то замкнена система є стійкою

3.4. Логарифмічно-частотні характеристики

Передаточна функція розімкненої системи складається з інтегруючої та двох аперіодичних ланок. Побудуємо ЛАХ та ЛФХ нашої розімкненої системи (рис.3.4.1):

Контрольна точка:

Визначимо граничні частоти: ,

Вираз для ЛФХ: ,

Обчисливши вираз для , маємо (табл.3.4.1):

Табл.3.4.1

	0,01	0,1	0,2	0,5	1	2	5	10	20	50	100	200	500	1000
	-90	-91	-93	-97	-105	-118	-146	-168	-188	-217	-238	-253	-263	-266

По ЛЧХ визначимо, що система майже стійка, бо має запаси стійкості, але вона перетинає вісь під нахилом -40дБ/дек, тому необхідно виконати корекцію системи.

Виконаємо корекцію заданої системи.

При виконанні корекції використаємо метод Солодовнікова, який використовує послідовну корегуючи ланку.

ЛАЧХ незмінної частини системи складається з трьох асимптот. Побудуємо бажану ЛАЧХ. Будемо вважати, що порядок астатизму і передаточний коефіцієнт ЛАЧХ незмінної частини системи змінювати не потрібно, тому низькочастотною асимптотою бажаної ЛАЧХ буде низькочастотна асимптота ЛАЧХ незмінної частини системи. Будемо також вважати, що скорегована система повинна задовольняти таким показникам якості:

час регулювання ;

перерегулювання .

Для цих показників по номограмах Солодовнікова визначаємо і , за якими обчислюємо частоту зрізу бажаної ЛАЧХ:

Рис.3.4.1

Через цю точку проводимо середньочастотну асимптоту бажаної ЛАЧХ із нахилом -20дБ/дек. Далі по номограмах для визначаємо, що необхідний надлишок фази 40 градусів при ординатах , що лежать у межах 14дБ. Високочастотною асимптотою бажаної ЛАЧХ буде високочастотна асимптота ЛАЧХ незмінної частини системи.