Курсовая работа: Одновісний гіроскопічний стабілізатор

Визначимо передаточну функцію системи за похибкою:

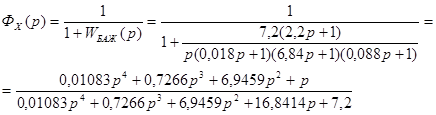
Знайдемо коефіцієнтипохибок , , поділивши поліном чисельника на поліном знаменика функції :

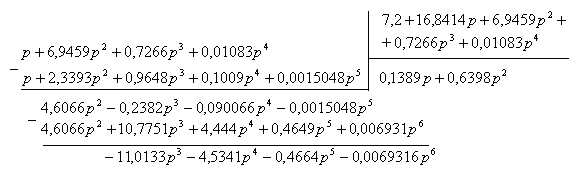
Усталена похибка при гармонічній вхідній дії має вигляд:

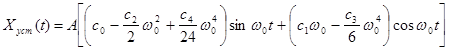
в нашому випадку:

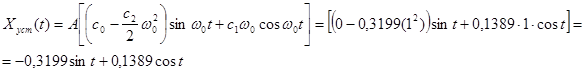
Графік усталеної похибки представлений на рис. 3.8.1.

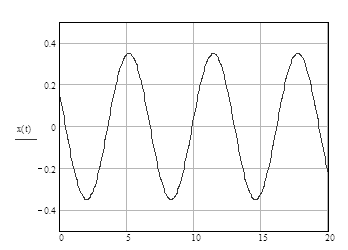
Рис.3.8.1

3.9. Моделювання

Змоделюємо реакцію системи на одиничний вхідний сигнал до корекції (рис.3.9.1, 3.9.2)та після неї (рис.3.9.3, 3.9.4) в середовищі MathLab.

Рис.3.9.1

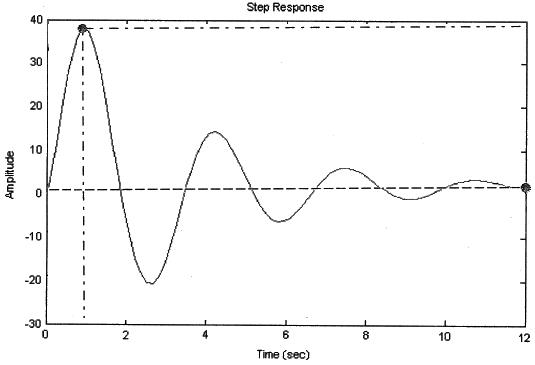
Рис.3.9.2

Рис.3.9.3

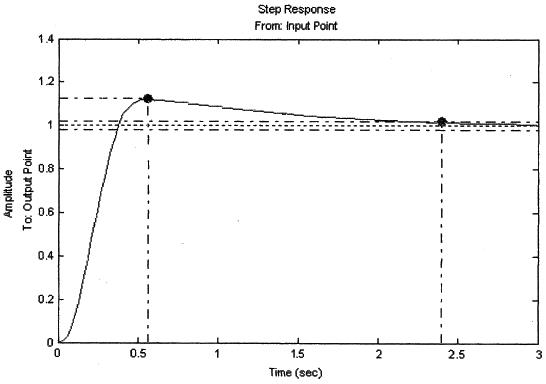
Рис.3.9.4

При моделюванні САК до корекції виявлено, що система наближається до стійкої.

При моделюванні перехідної характеристики скорегованої САК виявлено, що система стійка, час регулювання складає , перерегулювання .

4. Аналіз дискретної САК

4.1 Визначення періоду дискретизації

Визначимо період дискретизації імпульсного елементу, в якості формувача імпульсів використаємо екстраполятор нульового порядку.

Використовуючи ЛАЧХ розімкненої системи, визначимо період дискретизації: ЛАЧХ перетинає вісь -20дБ при . Тоді за теоремою Котельникова: де циклічна частота обирається рівною . Отримаємо і період дискретизації рівний .

4.2. Передаточні функції

Досліджуємо систему, що зображена на рис.4.2.1.

Рис.4.2.1

Визначимо дискретну передаточну функцію розімкненої та замкнутої ДСАК відносно вхідної дії: