Курсовая работа: Операторные уравнения

.

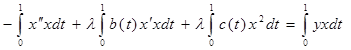Заметим, с учетом граничных условий:

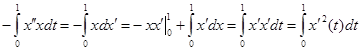
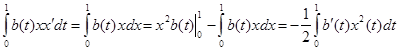
Подставим полученные интегралы и сгруппируем относительно λ:

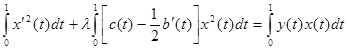(5)

Произведем оценку всех трех слагаемых в этом равенстве.

Докажем, что 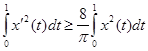. (6)

Заметим, что 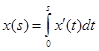, и значит по неравенству Коши – Буняковского:

.

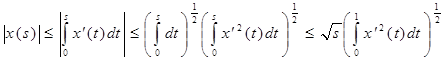Точно так же:

.

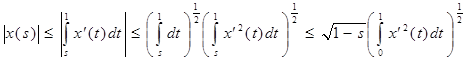Перемножим эти неравенства:

. (6*)

Отсюда, замечая, что 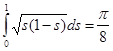, получим

.

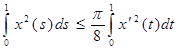
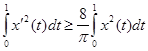Далее 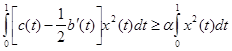(7)

– это следует из предположения (*).

Последний интеграл равенства (5) можно оценить, используя скалярный квадрат:

, где .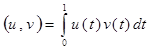

Для любого ε > 0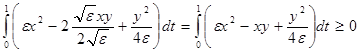

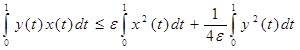. (8)

Используя полученные неравенства (6), (7), (8) и подставляя их в равенство (5), получаем:

,

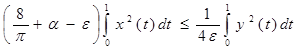считая ε > 0 достаточно малым, имеем

.

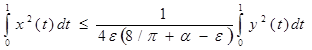Выберем и получим

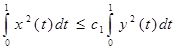, где .

Возвращаясь снова к равенству (5), получим следующую оценку: