Курсовая работа: Операторные уравнения

§4. Абстрактные функции

Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.

Рассмотрим функцию x() с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.

Пусть x() определена в окрестности точки 0, за исключением, быть может, самой точки 0. Элемент а Î X будем называть пределом функции x() при →0 и записывать

при →0,

если при →0.

Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра.

Рассмотрим в нормированном пространстве X ряд вида , где xк Î X, а – вещественное или комплексное переменное. Поскольку можно ввести новую переменную –0 = , то в дальнейшем мы полагаем 0 = 0 и рассматриваем степенные ряды вида

(1)

Конечная сумма называется частичной суммой степенного ряда (1).

Пусть – множество всех точек , для которых ряд (1) сходится. называется областью сходимости ряда (1).

Сумму ряда (1) при Î обозначим через S() (это абстрактная функция, определенная на со значениями в X), при этом будем писать

, при Î.

Последнее равенство означает, что Sn() → S() при n→∞ для всех Î.

Очевидно, область сходимости любого степенного ряда (1) не пуста, так как 0 Î. Как и в случае скалярных функций, справедлива следующая теорема.

Теорема 10 (Абель). Пусть0 ≠ 0 и 0 Î, тогда круг содержится в . Во всяком круге Sr(0), где r < , ряд (1) сходиться абсолютно и равномерно относительно .

Теорема 11. Пусть два степенных ряда равны в круге SR(0), R>0:

;

тогда равны все их коэффициенты: (k=0, 1, 2, …)

Дифференцирование абстрактных функций

Пусть функция числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.

По определению производной x’(λ0) функции x(λ) в точке λ0 называется предел

,

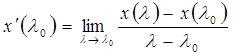если этот предел существует (и конечен). Если имеет производную в точке λ0, то она называется дифференцируемой в этой точке.

§5. Аналитические абстрактные функции и ряды Тейлора

Абстрактную функцию x() будем называть аналитической при =0, если она представима в некоторой окрестности точки =0 сходящимся степенным рядом:

(1)

с ненулевым радиусом сходимости.

Теорема 12. Если x() – аналитическая абстрактная функция при =0, то x() непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).