Курсовая работа: Определение энергосиловых параметров

для стали марки 10 при : ;

- термомеханический коэффициент, учитывающий влияние температуры,

для стали марки 10 при : ;

-термомеханический коэффициент, учитывающий влияние скорости деформирования, для стали марки 10 при : .

МПа

МПа

2.3. Определение контактных напряжений

Контактное напряжение состоит из двух составляющих:

- нормальное касательное напряжение σz, направление вектора которого совпадает с нормалью к площадке приложения сил,

- касательное контактное напряжение τк, действующее в плоскости площадки приложения сил. (см. рисунок 5)

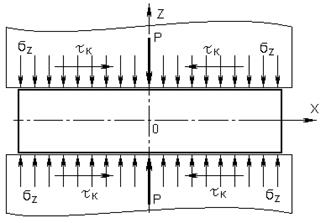
Рисунок 5. Кинематическая схема при осадке

Направление элементарных сил трения на контактной поверхности, а следовательно, и контактных касательных напряжений показано на рисунок 5. Согласно правилу знаков касательные напряжения на половине фигуры справа от оси будут отрицательны, а слева – положительны. В силу симметрии сечения относительно координатных осей достаточно рассматривать лишь первый квадрант.

Выделим в теле бесконечно малый объём плоскостями, параллельными оси z на расстоянии x и x+dx от начала координат; длину этого объёма примем равной единице. (см. рисунок 6). На выделенный объём действуют нормальные напряжения σz, σx, σx+dσx и касательное напряжение τxz. Согласно второму допущению принимаем, что σz и σx не зависят от координаты z, т.е. постоянны по высоте и зависят только от координаты x. Тогда второе дифференциальное уравнение равновесия

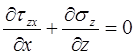тождественно обращается в нуль.

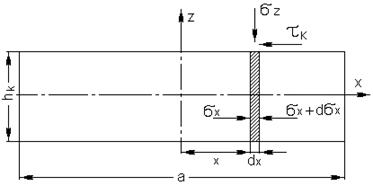
Рисунок 6. Схема к определению усилия осадки

Касательное напряжение τxz, переменное по ширине и высоте, на контактной поверхности равно τк - касательному напряжению, обусловленному

трением тела об инструмент. Величина уменьшается при удалении от контактной поверхности и вследствие симметрии на середине высоты полосы равна нулю. Примем, что τxzзависит от высоты полосы линейно, т.е.

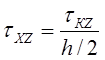. (10)

Тогда 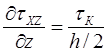. (11)

Подставив значение в первое уравнение равновесия, получим:

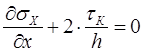(12)

Так как касательное напряжение на контактной поверхности обусловлено трением металла об инструмент, естественно его определить на основании закона Кулона - Амонтона:

(13)

Тогда (14)

Уравнение пластичности для плоского деформированного состояния для нашего случая представим в виде:

(15)

Разность нормальных напряжений зависит от касательного напряжения.

Если касательное контактное напряжение не зависит от нормальных напряжений, то разность нормальных напряжений – величина постоянная. В частных случаях, когда τк и τxz равны нулю (трение отсутствует), σxи σz являются главными напряжениями и выражение (15) превращается в уравнение (6):