Курсовая работа: Оптимізація завозу–вивозу вантажів у вузлі взаємодії залізничного, річкового і автомобільного транспорту

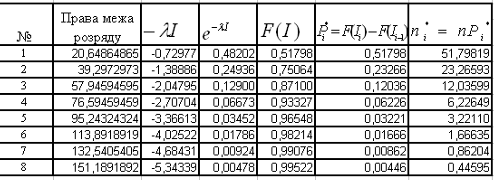
Теоретична ймовірність Р_і ^* інтервалів визначеної величини в їх загальної сукупності дорівнює:

Але так як К=1, то

Обчислення приведенні в таблиці 1.4.

Таблиця 1.4

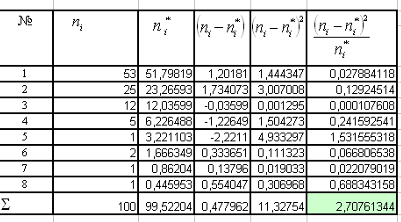
Складаємо таблицю 1.5 з якої знайдемо спостережне значення критерію.

Таблиця 1.5

За таблицею критичних точок рівню значущості a=0,05 і числу степінь волі r=s-3 (s – число розряду) знаходимо критичну точку правосторонню критичної області .=11,1 , бо число ступенів свободи 5.

Так як =2,7 , то <, бо 2,7 < 11,1. Отже, нема підстави відкидати гіпотезу про ерланговський закон розподілу вхідного потоку потягів на станцію.

1.4 Визначення параметрів вхідного потоку, аналізуючи кількість поїздів, які прибувають на станцію за годину

Складаємо статистичний ряд розподілення величини а - кількості поїздів за годину.

Величина а є випадковою до того ж дискретного типу.

М(а) = ∑a_i P_i (1.6)

M(a² ) = ∑a² _i P_i (1.7)

D(а) = М(а² ) - (М(а))² (1.8)

(1.9)

Розрахунок приведено у таблиці 1.6.

Таблиця 1.6 – Статистичний ряд розподілення кількості поїздів за годину

№	ai	ni	Pi	M(a)	M(a2 )
1	0	4	0,09091	0	0
2	1	9	0,20455	0,20454545	0,20455
3	2	14	0,31818	0,63636364	1,27273
4	3	10	0,22727	0,68181818	2,04545
5	4	4	0,09091	0,36363636	1,45455
6	5	1	0,02273	0,11363636	0,56818
7	6	1	0,02273	0,13636364	0,81818
8	7	1	0,02273	0,15909091	1,11364
Σ	44	1	2,29545455	7,47727273

Параметри розподілення величини a такі

М(а) = ∑a_i P_i = 2,29 поїзда

M(a² ) = ∑a² _i P_i = 7,47 поїздів

D(а) = М(а² ) - (М(а))² = 7,47 – 2,29² = 2,23 поїздів

поїздів

1.5 Побудова графіку статистичного розподілу величини поїздів і функції їх розподілу

При аналізі багатьох випадкових дискретних процесів використовують розподіл Пуассона, і ми зробимо припущення, що потік поїздів підпорядкований Пауссонівському розподілу. Імовірність того, що в одиницю часу (t) відбудеться рівно а випадків визначається за формулою:

, (1.10)