Курсовая работа: Оптимізація завозу–вивозу вантажів у вузлі взаємодії залізничного, річкового і автомобільного транспорту
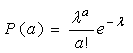 (1.11)
(1.11)
де λ - середня кількість випадків за одиницю часу.
λ = М(а) = 2,29 поїзда/год.
Визначимо по закону Пуассона розподіл ймовірностей.
Розрахунок зведемо у табл. 1.7.
Таблиця 1.7 – Розподіл ймовірностей по закону Пуассона
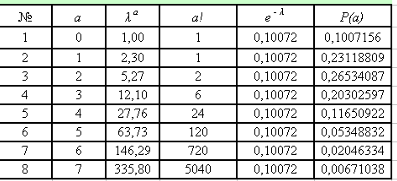
На засаді даних, розрахованих у табл.1.7 і табл.1.6 будуємо імовірнісну (Ра) і статистичну (Рi ) криві.
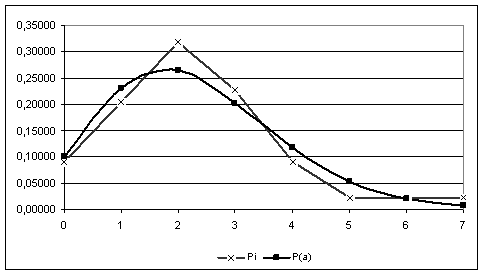
Рисунок 1.2 – Графік імовірнісної і статистичної кривої
Проаналізувавши графіки статистичної і імовірнісної кривих можна зробити висновок, що вхідний потік поїздів може бути описано законом Пуассона.
1.6 Визначення параметрів розподілення кількості вагонів у поїзді
Будемо розглядати кількість вагонів у поїзді як випадкову дискретну величину, яка змінюється в межах від 45 до 55 вагонів. Для визначення параметрів необхідно збудувати статистичний ряд розподілення кількості вагонів у потязі.
Таблиця 1.8 – Статистичний ряд розподілення кількості вагонів у потязі
| Кількість | Частота спостережень, ki | Pi = ki / Σki | mi · Pi | mi 2 ·Pi |
| вагонів, mi | ||||
| 45 | 8 | 0,07921 | 3,56436 | 160,39604 |
| 46 | 8 | 0,07921 | 3,64356 | 167,60396 |
| 47 | 10 | 0,09901 | 4,65347 | 218,712871 |
| 48 | 6 | 0,05941 | 2,85149 | 136,871287 |
| 49 | 8 | 0,07921 | 3,88119 | 190,178218 |
| 50 | 8 | 0,07921 | 3,96040 | 198,019802 |
| 51 | 13 | 0,12871 | 6,56436 | 334,782178 |
| 52 | 13 | 0,12871 | 6,69307 | 348,039604 |
| 53 | 12 | 0,11881 | 6,29703 | 333,742574 |
| 54 | 11 | 0,10891 | 5,88119 | 317,584158 |
| 55 | 4 | 0,03960 | 2,17822 | 119,80198 |
| Σ | 101 | 1 | 50,16832 | 2525,73267 |
Проведемо розрахунок параметрів розподілення кількості вагонів у поїзді
M(m)=![]() = 50,17 вагонів;
= 50,17 вагонів;
![]() 2525,73 вагонів
2525,73 вагонів![]() ;
;
![]() вагонів
вагонів![]() ;
;
![]() вагонів;
вагонів;
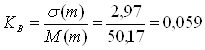
1.7 Визначення параметрів тривалості обробки складів поїздів у парку прийому
Тривалість обробки визначається за формулою
|
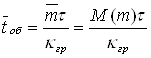
де ![]() - середній час обробки одного вагону, (
- середній час обробки одного вагону, (![]() =0,97хв);
=0,97хв);
![]() - кількість груп в бригаді ПТО,
- кількість груп в бригаді ПТО, ![]() =4
=4
![]()
![]() ,
,
![]()
![]() ,
,
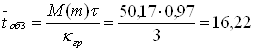
![]() ,
,
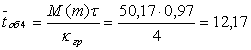
![]() ;
;