Курсовая работа: Открытые сети с многорежимными стратегиями обслуживания и информационными сигналами

Доказательство. Так как - непрерывная функция от и , то доказательство следует из результата [90], полученного в этой работе с помощью теоремы Брауэра о неподвижной точке.

В дальнейшем будем предполагать, что существует решение (4.1.1),(4.1.2), для которого все . Для того, чтобы это выполнялось, надо наложить некоторые условия на маршрутизацию заявок в сети. Например, такое решение будет заведомо существовать, если при каждом выполняется условие . На самом деле можно наложить гораздо менее жесткие условия. Всюду в дальнейшем под словами решение (4.1.1),(4.1.2) будет пониматься именно такое решение. Это предположение гарантирует неприводимость марковского процесса на фазовом пространстве , где .

Изолированный узел в фиктивной окружающей среде .

Рассмотрим изолированный -й узел в фиктивной окружающей среде, считая, что в него поступают два независимых пуассоновских потока: положительных заявок с параметром и отрицательных заявок с параметром , где и найдены из системы уравнений трафика (4.1.1),(4.1.2). Окружающая среда является фиктивной потому, что в самой сети потоки заявок на ее узлы не являются простейшими. Необходимым и достаточным условием обратимости, а, значит, и квазиобратимости изолированного узла является условие

Действительно, модифицируя доказательство леммы 2.2, получаем, что при его выполнении произведение интенсивностей, ведущих из любого состояния в это же самое состояние по ребрам элементарного квадрата по и против часовой стрелки совпадают для марковского процесса, описывающего такой изолированный узел. Условия (4.1.3) выполняются, в частности, если интенсивности переходов из одного режима в другой не зависят от состояния узла. Обозначая через финальные стационарные вероятности его состояний, запишем уравнения обратимости для изолированного узла:

Из этих уравнений легко определяются стационарные вероятности состояний изолированного узла в фиктивной окружающей среде:

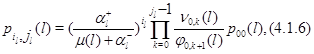
где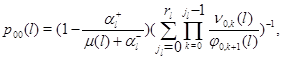

и, как всегда, предполагается, что произведение, в котором нижний индекс больше верхнего, равно 1.

Согласно эргодической теореме Фостера [82] для эргодичности марковского процесса, описывающего изолированный узел в фиктивной окружающей среде, достаточно существования нетривиального неотрицательного решения системы уравнений равновесия такого, что

Если

то в силу (4.1.6) ряд сходится как сумма геометрической прогрессии со знаменателем, меньшим единицы. При выполнении условия

интенсивность выхода из состояния ограничена:

Поэтому при выполнении условий

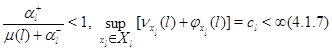
сходится ряд и по эргодической теореме Фостера марковский процесс, описывающий изолированный узел в фиктивной окружающей среде эргодичен.

Основной результат . Пусть - интенсивность перехода процесса из состояния в состояние , - интенсивность его выхода из состояния , - вектор , у которого все кроме равны 0, а , и все , - вектор , у которого все и все кроме равны 0, а . Очевидно, интенсивности перехода процесса имеют следующий вид: