Курсовая работа: Оценивание смещения статистики взаимной спектральной плотности многомерного временного ряда

, .

Корреляционной функцией случайного процесса , , называется функция вида

, .

Ковариационной функцией случайного процесса , , называется функция вида

.

Заметим, что если , то , .

Смешанным моментом го порядка , , случайного процесса , , называется функция вида

, , .

Заметим, что

, .

Пусть - значения случайного процесса в точках .

Смешанный момент го порядка, , можно также определить как

, , .

Смешанным семиинвариантом ( кумулянтом ) го порядка, , случайного процесса , , называется функция вида

, , ,

которую также будем обозначать как .

Между смешанными моментами и смешанными семиинвариантами го порядка, , существуют связывающие их соотношения, которые имеют вид

(1.1)

(1.2)

суммирование по всевозможным разбиениям множества .

Спектральной плотностью случайного процесса , , называется функция вида

=, ,

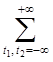
при условии, что

.

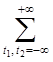
Из определения видно, что спектральная плотность непрерывная, периодическая функция с периодом, равным по каждому из аргументов.

Семиинвариантной спектральной плотностью го порядка, , случайного процесса , , называется функция вида