Курсовая работа: Оценивание смещения статистики взаимной спектральной плотности многомерного временного ряда

при условии, что

.

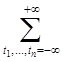
Лемма 1. Для любого целого справедливо соотношение

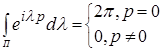(1.3)

Теорема 1. Для смешанного семиинварианта го порядка, , случайного процесса справедливы представления

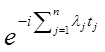
, (1.4)

Доказательство. Домножая обе части соотношения (1.1) на

, ,

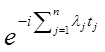и интегрируя обе части полученного неравенства по на , получим

.

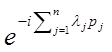
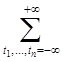
Используя лемму 1, получим при требуемый результат. Теорема доказана.

Лемма 2. Если функция интегрируема и периодична с периодом , то для любого действительного имеет место соотношение

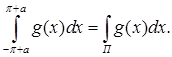
Доказательство . Предположим, что >0. Можно записать

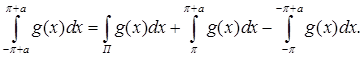
В третьем слагаемом правой части последнего равенства сделаем замену переменных интегрирования и, учитывая периодичность с периодом функции , получаем требуемое. Случай, когда <0, доказывается аналогично. Лемма доказана.

Спектральной плотностью случайного процесса , , называется функция вида

=, ,

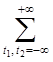
при условии, что

.

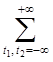
Из определения видно, что спектральная плотность непрерывная, периодическая функция с периодом, равным по каждому из аргументов.

2. ОЦЕНИВАНИЕ СМЕЩЕНИЯ СТАТИСТИКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ

Рассмотрим действительный стационарный в широком смысле случайный процесс,, с математическим ожиданием , , взаимной ковариационной функцией , и взаимной спектральной плотностью .

Предположим, имеются Т последовательных, полученных через равные промежутки времени наблюдений за составляющей , рассматриваемого процесса . Как оценку взаимной спектральной плотности в точке рассмотрим статистику

(2.1)

где , - произвольная, не зависящая от наблюдений четная целочисленная функция, для , а

(2.2)

s – целое число, - целая часть числа .

Статистика , называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением