Проверку однородности дисперсий при полученном виде дублирования проводят с помощью G – критерия Кохрена:

G_расч =, (1.11)

где - сумма всех дисперсий;

S² _max – наибольшая из всех найденных дисперсий.

G_расч =13,98/112,22= 0,125

При q=0,05 и f=n-1=3, G_табл =0,29[1. табл. Ж1].

Так как G_расч <G_табл , то гипотеза об однородности дисперсии опытов принимается.

1.2.3 Расчет дисперсии воспроизводимости

Дисперсия воспроизводимости определяется по формуле:

S^{2 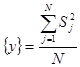,} (1.12)

где N- число опытов.

S² {y}=112,22/14=8,02

Число степеней свободы для данной процедуры:

f_y =N(n-1) (1.13)

f_y =3*14=42.

2 Построение математической модели

2.1 Расчет коэффициентов регрессии

По результатам В₃ -план построим математическую модель:

Y=b₀ +b₁ *x₁ +b₂ *x₂ +b₃ *x₃ +b₁₁ *x₁ ² +b₂₂ *x₂ ² +b₃₃ *x₃ ² +b₁₂ *x₁ *x₂ +b₁₃ *x₁ *x₃ +b₂₃ *x₂ *x₃

Таблица 2.1 – Матрица для расчета коэффициентов регрессии

№ опыта	X0	X1	X2	X3	X11	X22	X33	X12	X13	X23	Yij	Ŷij
1	2	3	4	5	6	7	8	9	10	11	12	13
1	1	1	1	1	1	1	1	1	1	1	16.02	15.92
2	1	-1	1	1	1	1	1	-1	-1	1	33.66	33.60
3	1	1	-1	1	1	1	1	-1	1	-1	13.1	12.95
4	1	-1	-1	1	1	1	1	1	-1	-1	27.36	27.00
5	1	1	1	-1	1	1	1	1	-1	-1	33.38	33.74
6	1	-1	1	-1	1	1	1	-1	1	-1	59.32	59.47
7	1	1	-1	-1	1	1	1	-1	-1	1	34.76	34.82
8	1	-1	-1	-1	1	1	1	1	1	1	56.82	56.92
9	1	1	0	0	1	0	0	0	0	0	19.42	19.25
10	1	-1	0	0	1	0	0	0	0	0	38.96	39.13
11	1	0	1	0	0	1	0	0	0	0	30.58	30.22
12	1	0	-1	0	0	1	0	0	0	0	27.1	27.46
13	1	0	0	1	0	0	1	0	0	0	23.62	24.29
14	1	0	0	-1	0	0	1	0	0	0	48.84	48.17

Используя матрицу базисных функций, табл. 2.1, коэффициенты регрессии определяем по следующим формулам:

- свободного члена:

b₀ =-; (2.1)

- линейных коэффициентов регрессии:

b_i = ; (2.2)

- квадратичных коэффициентов:

b_ii = ; (2.3)

- коэффициентов при парных взаимодействиях:

b_iu = . (2.4)

2.2 Расчет дисперсий коэффициентов регрессии

Формулы для определения дисперсий: - дисперсия оценки свободного члена:

S² {b₀ }= ; (2.5)