Курсовая работа: Планы второго порядка, реализация В3-плана

- дисперсия оценки линейных коэффициентов регрессии:

S² {b_i }= ; (2.6)

S² {b_i }=0,80

- дисперсия оценки квадратичных коэффициентов регрессии:

S² {b_ij }=; (2.7)

S² {b_ii }=3,26

- дисперсия оценки коэффициентов при парных взаимодействиях:

S² {b_iu }= . (2.8)

S² {b_iu }=1,00

2.3 Проверка значимости коэффициентов регрессии

Для оценки значимости регрессии используем t – критерий Стьюдента. По следующим формулам определяются расчетные значения t – критерия Стьюдента:

t_{расч i} =, (2.9)

где S{b_i }= - среднеквадратическое отклонение соответствующих дисперсий коэффициентов регрессии;

t_{расч ii} =, (2.10)

t_{расч iu} =. (2.11)

Таблица 2.2 - Проверка значимости коэффициентов регрессии

обозначение коэффициентов регрессии	значение коэффициентов регрессии	Расчетные значения t-критерия Стьюдента
			b0	29.98	9
			b1	-9.94	-12
			b2	1.38	2
b3	-11.94	-15
b11	-0.79	0
b22	-1.14	0
b33	6.25	2
b12	-0.91	-1
b13	2.01	2
b23	1.01	1

По t – критерию Стьюдента, по заданному уровню значимости (q=0,05) ичислу степеней свободы (f_y =42), связанному с дисперсией воспроизводимости, находим табличное значение t – критерия Стьюдента [1. табл. Д1]:

t_табл =2,02

Если t_расч , > t_табл , то соответствующий коэффициент регрессии значим. Незначимые коэффициенты регрессии должны быть исключены из математической модели. Однако, в данной расчетной части с целью сохранения единообразия расчетов процедура исключения не проводится.

Получена следующая математическая модель в нормализованных обозначениях факторов:

Y=101,65+42,425х₁ +2,9х₂ +15,5х₃ +8,4х₁₁ -2,98х₂₂ -2,46х₃₃₊ 2,22х1х2+6,28х1х3+1,11х₂ х₃

2.4 Проверка модели на адекватность

Для проверки адекватности модели используют дисперсию адекватности S² _aq , процедура расчета которой зависит от вида дублирования опытов. Так как в нашем случае дублирование равномерное, то дисперсия адекватности рассчитывается по формуле:

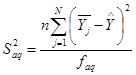
(2.12)

где f_aq =N-p=14-10=4,

где p – число оцениваемых коэффициентов;

S² _aq = 0,39

Затем, по F – критерию Фишера для уровня значимости q=0,05 проверяется однородность S² _aq дисперсии адекватности (с числом степеней свободы f_aq ):

F_расч = (2.13)

F_расч = 0,39/8,02=0,049

По таблице значения F - критерия Фишера [1. табл. Е1]: