Курсовая работа: Плоскі діелектричні хвилеводи для ТІ поляризації

Одержали ще одне хвильове рівняння, у скалярному виді. Його рішення буде мати вигляд: , де - комплексна постійна поширення, а k – одиничний вектор у напрямку поширенні хвилі. Дійсна частина постійної поширення являє собою коефіцієнт поглинання по амплітуді, а мнима частина – модуль хвильового вектора .

У випадку плоскої хвилі вектори E,H,k ортогональні й відношення модулів векторів E,H :

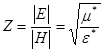
є характеристичний хвильовий імпеданс.

2. Параметри середовища

При описі поширення хвилі в середовищі, крім і часто використовуються інші параметри , наприклад : - довжина хвилі у вакуумі, що відрізняється від - довжини хвилі в середовищі. - показник переломлення в середовищі.

3. Граничні умови

Виходячи з умов Максвелла в інтегральній формі, можна визначити умови для векторів E,D,H,B на границі роздягнула двох середовищ, з різними й .

(19)

(20)

(21)

(22)

Де індексом i позначені частки векторів, дотичні до поверхні роздягнула двох середовищ 1 і 2. А індексом n – частки нормальні до цієї поверхні. Величина J – щільність поверхневих струмів провідності, а - щільність електричних зарядів, причому в тих випадках, які ми будемо розглядати, вони дорівнюють нулю. Цього ж рівняння можна представити у векторній формі, якщо ввести в розгляд одиничний вектор нормалі до границі роздягнула.

У такий спосіб:

4. Формули Френеля

Нехай А - амплітуда електричного вектора поля падаючої хвилі. Будемо вважати її комплексною величиною з фазою , рівної постійної частини аргументу хвильової функції. Змінна її частина має вигляд:

Тепер розкладемо вектор на паралельну й перпендикулярну тридцятилітні:

Компоненти магнітного вектора виходять зі співвідношення

Звідси

Граничні умови й вимагають щоб на границі тангенціальна тридцятилітні векторів E і H були безперервні. Отже, потрібно зажадати виконання наступних співвідношень

Тепер можна одержати важливі співвідношення (рівняння):