Курсовая работа: Плоскі діелектричні хвилеводи для ТІ поляризації

У результаті підстановки цих рівнянь в

можна одержати хвильове рівняння для електричного компонента поля:

(33).

Одержали рівняння поширення, що описує, хвилі в оптичному хвилеводі. Це рівняння з змінними і його рішення варто шукати у вигляді добутку двох функцій, одна й з яких залежить тільки від y, а друга тільки від z. Розподіл амплітуди поля по координаті x передбачається рівномірним.

Т.е. можна записати:

, де , а

Оскільки ліва й права частини вираження залежать від різних змінних, то рівність може дотримуватися тільки в тому випадку, коли кожна із частин рівності є константою. Нехай ця константа позначена , одержимо:

,

для i-ой середовища (усього 3 середовища)

Конкретний вид функції Y(y) визначається із цього рівняння з урахуванням граничних умов і описує розподіл амплітуд фаз у поперечному перерізі шару й прилягаючих середовищ. Повний же вид рішення визначається як добуток Y(y)Z(z) і з урахуванням тимчасової залежності має вигляд

.

Таким чином, рішення має вигляд гармонійної хвилі, що поширюється уздовж осі Y і має амплітудний розподіл Y(y) у напрямку, поперечному стосовно напрямку поширення.

Отже, потрібно знайти граничні умови, що задовольняють рівнянням безперервності дотичних E і H тридцятимільйонний компонент електромагнітного поля для ТІ хвиль мають вигляд:

при y=0

при y=-h.

Помітимо, що умови безперервності H- на границях еквівалентна умовам безперервності похідних від розподілу E- поля на границях шарів 1 і 2, 2 і 3. Нехай у розглянутій системі із трьох шарів виконується необхідна умова існування режиму, тобто . Фізично це означає, що хвилі, що біжать у шарі 2 можуть випробовувати повне внутрішнє відбиття від границь із шарами 1 і 3. Для рішення рівнянь розглянемо величину . Якщо величина виявиться негативної, то рішення являє собою експоненту з дійсним показником. Якщо ж ця величина - позитивна, то рішення являє собою гармонійну функцію або експоненту із мнимим показником. Розглянемо властивості рішень:

Умова А. .

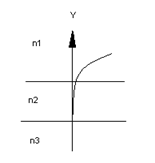
При цьому свідомо виконуються умови й , і з рівнянь (15-17) треба, що у всіх трьох областях. Очевидно, що є експонентною функцією у всіх трьох областях. З огляду на необхідність безперервності похідній розподілу поля на границях роздягнула між шарами, одержимо розподіл поля, що необмежено зростає при видаленні від границі між шарами хвилеводу. Отже, рішення, що відповідають області А, фізично нездійсненна.

Умова В. .

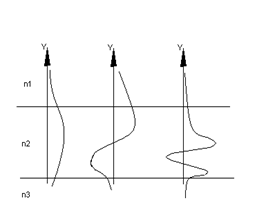
В області 2 рішення може бути представлене у вигляді гармонійної функції, оскільки , при цьому розподіл поля по координаті в у перетині шару 2 може мати характер парної або непарної функції.

В областях рішення буде мати вигляд експонент із дійсним показником ступеня. Очевидно, що фізично реалізований випадок відповідає експонентам, що спадають при видаленні від границі 1 у позитивному напрямку й від границі 3 у негативному напрямку. Як видно, у цьому випадку максимальна напруженість поля спостерігається усередині центрального шару хвилеводу. Напруженість поля спадає при видаленні від його границь, при цьому основна частка енергії хвилі переноситься в самому шарі 2 і прилеглих областях шарів, що обрамляють, 1 і 3, без випромінювання в навколишній простір. Такий режим називається хвиле водним, а центральний шар 2 часто називають несучим шаром хвилеводу.

Умова С. і, мабуть, .

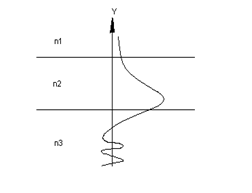
Рішення має експонентний характер в області 1 і гармонійний характер в областях 2 і 3. Поле є експоненціальне спадаючої при видаленні від границі в середовищі 1. поява осциляції в середовищі 3 може бути інтерпретоване як результат інтерференції двох плоских електромагнітних хвиль, що біжать: однієї хвилі - випромінюваної із хвилеводу, інший, рівної по амплітуді, що набігає на хвилевід з нескінченності. Припущення про існування хвилі, що набігає, знадобилося тут, щоб зберегти стаціонарність завдання уздовж осі z, тобто як би компенсувати втрати енергії на випромінювання , що з'являється при . Такі моди називають випромінювальними модами підложки.

Умова D. .