Курсовая работа: Порівняльний аналіз ефективності та складності прямих алгоритмів сортування масивів

Аналіз алгоритмів на основі прямого обміну. Розглянемо спочатку чисту "бульбашку". Для "камінця" оцінки будуть такими ж самими. Зрозуміло, що кількість порівнянь ключів C_i на i -ому проході не залежить від початкового розміщення елементів і дорівнює N-i . Таким чином

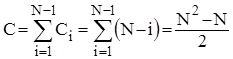
Кількість же перестановок залежить від стартової впорядкованості масиву. В найкращому випадку початково-впорядкованогомасиву M_i =0 ; в найгіршому випадку зворотно-впорядкованогомасиву M_i =C_i *3; для довільного масиву рівноймовірно можливе значення M_i =C_i *3/2. Тому для оцінки ефективності алгоритму по перестановках можна скористатися наступними співвідношеннями:

;

;

.

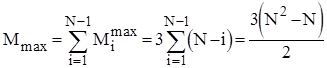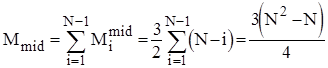Очевидно, що і цей алгоритм, аналогічно з іншими прямими методами, описує процес стійкого сортування.

Розглянемо тепер покращений варіант "шейкерного" сортування. Для цього алгоритму характерна залежність кількості операцій порівняння від початкового розміщення елементів в масиві. В найкращому випадку вже впорядкованої послідовності ця величина буде . У випадку зворотно-впорядкованогомасиву вона співпадатиме з ефективністю для чистої "бульбашки".

Як видно, всі покращення не змінюють кількості переміщень елементів (переприсвоєнь), а лише зменшують кількість повторюваних порівнянь. На жаль операція обміну місцями елементів в пам’яті є "дорожчою" ніж порівняння ключів. Тому очікуваного виграшу буде небагато. Таким чином "шейкерне" сортування вигідне у випадках, коли відомо, що елементи майже впорядковані. А це буває досить рідко.

2.5 Порівняння прямих методів сортування масивів

З метою порівняння методів сортування масивів було виконано тестування. Для кожного методу за алгоритмом було написано підпрограму на С++, після чого виконано тестування для масивів цілих чисел розміром 1024, 4096 та 16384. Результати тестування (кількість секунд з точністю до сотих) на комп’ютері Pentium-II/450 наведено у таблиці. Для кожного розміру масиву використовувалось 3 способи його побудови:

1) вже впорядкований за зростанням масив;

2) масив, впорядкований за спаданням;

3) масив з випадкових чисел.

24 4096 16384

Прямим включ. .00 0.05 0.00 .00 0.88 0.44 .00 14.01 6.98

Бінарним включ. .00 0.06 0.06 .00 0.61 0.28 .05 9.67 4.83

Прямим вибором .06 0.05 0.00 .50 0.49 0.49 .30 8.46 8.29

Бульбашка/Кам інець .00 0.11 0.11 .54 1.70 1.21 .73 27.79 19.45

Шейкерне .00 0.11 0.05 .00 1.71 0.99 .00 27.30 15.82

Результати показують, що оскільки швидкість сортування елементів є квадратичною, то час виконання практично однаковий, в той же час, для вже відсортованого масиву хороші результати продемонстрували сортування включенням та шейкерне сортування, у яких кількість операцій суттєво залежить від вигляду масиву. Отже, ці прості алгоритми сортування можна використовувати для „майже" відсортованих масивів, тобто, коли до відсортованого масиву додають m елементів (m<<n ).

Розділ ІІІ. Огляд функцій сортування із стандартної бібліотеки С++

Мова програмування С++ має в своєму складі функції, які дають змогу виконувати сортування елементів довільного типу без реалізації алгоритмів. Так, функція sort має декілька версій, в базовому її варіанті прототип виглядає наступним чином:

Void sort(Iterarot begin, Iterator end);

В якості параметрів функції використовуються два ітератори довільного доступу, призначені для роботи з окремим контейнером класу. З допомогою функціїsort дані контейнера впорядковуються, починаючи з елемента begin і закінчуючи елементом end (не включаючи його).

Оскільки вказівник на елемент масиву в С++ вважається ітератором довільного доступу, можна впорядкувати частину, або весь масив. Наприклад:

int mas [7]= {0, 10, 2, 0, 4, 15, 6}

//Елементи масиву будуть впорядковані. Зверніть увагу на те,

// що ім’я mas використовується в якості вказівника на перший