Курсовая работа: Порівняння характеристик аналогового та цифрового фільтрів

figure

hold on

plot(td(1,1:700), Signal_digital(1,1:700),'g-');

plot(td(1,1:700), Signd_out(1,1:700),'b-')

hold off;

grid on;

axis([0 0.08 -35 35]);

xlabel('t, c');

ylabel('Amplitude');

title ('Filtered and NOT filtered signals');

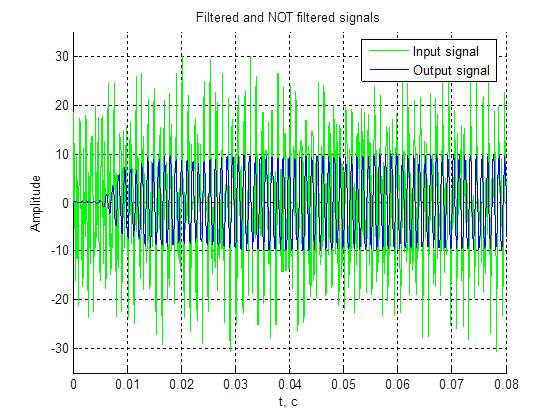
Рис. 13. Вхідний та вихідний сигнали.

2 .4 Побудова спектрів вхідного та вихідного сигналів

Побудуємо спектри вхідного та вихідного сигналів. Для побудови ряду використаємо дискретне перетворення Фур’є. Припустимо, що у нас задано функцію дискретної змінної на рівномірній гратці, тобто задані значення функції f k для скінченної послідовності значень аргументу x k = kh – таблиця функції { f k ; kh ; k = 0:: N } . Тут за допомогою позначено крок гратки – відстань між сусідніми вузлами. Перетворення Фур’є такої функції можна означити, як суму

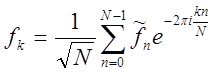
Наведені вище міркування про властивості значень нескінченного ряду Фур’є свідчать про недоцільність використання суми з кількох членів, більшою за кількість вузлів гратки. Можна також зауважити, що сума з більшою кількістю членів містила б більше інформації про функцію, ніж є в таблиці значень функції. Звичайно ж, обидва ці міркування не є доведеням можливості використання саме такої кількості членів – необхідно побудувати правило обчислення коефіцієнтів суми Фур’є і довести існування єдиного набору таких коефіцієнтів для функції дискретної змінної.

Для дійсних функцій і особливо при використанні програмних засобів, що не підтримують комплексних чисел, може бути доцільним використання дійсної форми перетворення Фур’є поданням функції у вигляді ряду по синусах та косинусах:

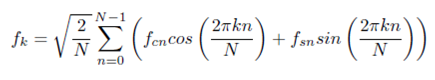
Для побудови спектрів використаємо середовище MatLab

k1=10;

k2=9;

k3=12;

phi1=pi;

phi2=pi/4;

phi3=pi/2;

W1=6000;

W2=10976;

W3=24387;

sign_freq=[W1 W2 W3];