Курсовая работа: Построение аналоговой ЭВМ для решения дифференциального уравнения шестого порядка

Введение

1. Выбор варианта задания

2. Основные этапы программирования задач

3. Моделирование левой части уравнения

3.1 Запись левой части уравнения

3.2 Расчет масштабных коэффициентов

3.3 Расчет напряжений начальных условий

3.4 Расчет коэффициентов передачи

4. Моделирование правой части уравнения

5. Расчет элементов схемы

5.1 Расчет элементов для операционных усилителей

5.2 Расчет элементов для схемы установки начальных условий

6. Расчет параметров с допустимой погрешностью

7. Описание принципиальной схемы

Заключение

ВВЕДЕНИЕ

Аналоговые вычислительные машины (АВМ) используют непрерывную форму представления информации и аналитический принцип ее переработки, при реализации которого каждой аналитической зависимости между математическими переменными соответствует подобное аналитическое описание связи между машинными переменными. Любая простейшая математическая операция в АВМ – сложение, умножение, интегрирование и т.д. – выполняется отдельным элементарным блоком машины, у которого аналитическая связь между входными и выходными физическими величинами подобна заданной аналитической зависимости.

Непрерывная форма представления информации и аналитический принцип ее переработки обеспечивают непрерывное решение математической задачи на АВМ и высокое быстродействие. Однако точность Работы АВМ ограничена точностью изготовления ее отдельных элементарных блоков и стабильностью их характеристик в процессе решения задачи. Указанные качества АВМ наряду с относительно малым временем и простотой подготовки задачи для машинного решения, простотой обслуживания и несложной конструкцией выгодно отличают АВМ от ЦВМ в тех применениях, когда не требуются высокая точность и универсальность. Особое значение современные АВМ и их отдельные устройства имеют для обеспечения задач моделирования динамических процессов, описываемых различными типами дифференциальных уравнений высоких порядков, и управления этими процессами.

1. ВЫБОР ВАРИАНТА ЗАДАНИЯ

Вариант курсовой работы формируется путем выбора соответствующих варианту конкретных значений коэффициентов для дифференциального уравнения с переменной правой частью из методических указаний.

Номер варианта выбирается по журналу - №12.

Для варианта №11 заданы следующие начальные значения:

Таблица 1

№	Е(В)	n	M	N	T(c)	DUдоп(%)
11	1	6	2	8	0,5	0,5

Где Е(В)— напряжение на входе первого интегратора в правой части уравнения;

n— степень дифференциального уравнения;

m— степень полинома правой части уравнения;

N— разрядность АЦП и ЦАП;

Т— время интегрирования;

DUдоп— погрешность решения уравнения.

Общий вид уравнения:

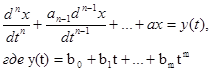
--> ЧИТАТЬ ПОЛНОСТЬЮ <--