Курсовая работа: Преобразование параллельного двоичного кода в код Хэмминга
В курсовой работе проверочную матрицу будем задавать с помощью элементов поля Галуа. Для формирования поля выбирается неприводимый порождающий полином степени r:
q(x) = x4 + x3 + 1.
Элементы поля находятся путем деления многочлена степени меньшей, чем n-1, на полином, являющийся неприводимым, т.е. на q(x).
Таким образом, получившиеся элементы поля приведены в таблице 1.
таблица 1 – Элементы поля Галуа
| αi | R(x) | HT |
| α0 | 1 | 1 0 0 0 |
| α1 | x | 0 1 0 0 |
| α2 | x2 | 0 0 1 0 |
| α3 | x3 | 0 0 0 1 |
| α4 | 1+ x3 | 1 0 0 1 |
| α5 | 1+x+ x3 | 1 1 0 1 |
| α6 | 1+x+x2 +x3 | 1 1 1 1 |
| α7 | 1+x+x2 | 1 1 1 0 |
| α8 | x+x2 +x3 | 0 1 1 1 |
| α9 | x2 +x3 | 0 0 1 1 |
| α10 | x+ x3 | 0 1 0 1 |
| α11 | 1 +x2 +x3 | 1 0 1 1 |
| α12 | 1+x | 1 1 0 0 |
| α13 | x+x2 | 0 1 1 0 |
| α14 | x2 +x3 | 0 0 1 1 |
Поскольку в качестве столбцов матрицы H кода Хэмминга выбираются все ненулевые двоичные числа, то матрица H – матрица степеней элемента поля α, т.е. H = [α0 , α1 , α2 , α3 ,…αn -1 ].
Итак, получаем проверочную матрицу полного кода Хэмминга (15, 11):

Чтобы в матрице информационные и проверочные двоичные символы были разделены, приведем проверочную матрицу H(15,11) к приведено-ступенчатому виду:

Чтобы получить матрицу Н кода Хэмминга с нужным числом информационных символов, в нашем случае k = 8, необходимо в проверочной матрице полного кода исключить любые T = 3 столбцов, относящиеся к информационным разрядам, т.е. исключить нужное число столбцов весом w≥2. Итак, исключим из матрицы H(15, 11) три столбца с максимальным весом.
Чем больше логических единиц в приписываемых строках проверочной матрицы, тем большей корректирующей способностью обладает разрабатываемый код, но тем больше будет иметь кодек сумматоров по модулю два и тем больше сложность его реализации. Следовательно, вычеркивание столбцов с максимальным весом приводит к уменьшению сложности вышеуказанных блоков. Проверочная матрица H укороченного кода (12, 8) имеет вид:

Главной функцией кодера является формирование проверочных уравнений, правило формирования которых определено проверочной матрицей H(12, 8) . В матрице H(12, 8) символы a1 , a2 , a3 …a8 – информационные, а a9 , a10 , a11 , a12 – проверочные, которые могут быть получены путем суммирования по модулю два определенных информационных символов.
Правило формирования проверочного символа для любой кодовой последовательности одинаково и определяется номерами позиций логических единиц в каждой строке проверочной подматрицы проверочной матрицы H(12, 8) . Так символ a1 формируется путем суммирования по модулю два информационных символов. Итак, устройство кодирования (кодер) реализует нижеследующие уравнения:
a9 = a1 + a2 + a3 + a6 ,
a10 = a2 + a3 + a5 + a6 + a7 ,
a11 = a3 + a4 + a7 + a8 ,
a12 = a1 + a2 + a4 + a5 + a8 ,
где под знаком "+" подразумевается суммирование по модулю два.
Используя полученную выше систему формирования проверочных символов, составим структурную схему кодера, представленную на рисунке 2:
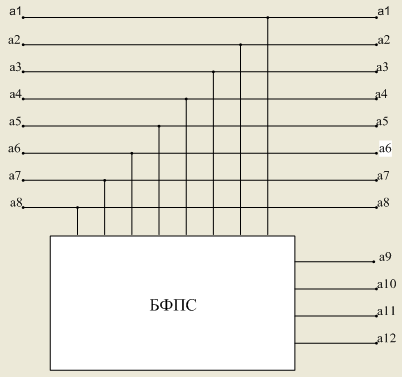
Рисунок 2 – Структурная электрическая схема кодера кода Хэмминга
Рассмотрим принцип работы структурной схемы.
На вход кодирующего устройства передаются в параллельном виде информационные символы a1 , a2 , a3 …a8 . Затем они поступают на блок формирования проверочных символов (БФПС), где из восьми информационных символов формируется 4 проверочных разряда в соответствии с уравнениями кодирования. Закодированная информация из кодирующего устройства передается в параллельном виде.
4. РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ ЭЛЕКТРИЧЕСКОЙ СХЕМЫ КОДЕРА
Так как функциональная схема служит для разъяснения и конкретизации видов процессов, происходящих в отдельных функциональных блоках, то в данном разделе основное внимание должно быть обращено на выбор и обоснование принципа построения каждого функционального блока кодека, представленного на структурной электрической схеме кодека.
Функциональная схема представляет собой гибрид структурной и принципиальной. Некоторые наиболее простые блоки отображаются на ней, как на структурной схеме, а остальные — как на принципиальной схеме. Функциональная схема дает возможность понять всю логику работы устройства, все его отличия от других подобных устройств, но не позволяет без дополнительной самостоятельной работы воспроизвести это устройство.
Функциональная схема кодера представлена на рисунке 4: