Курсовая работа: Применение метода ветвей и границ для задач календарного планирования

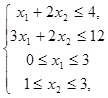(12) и 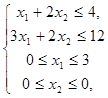(13).

Выполним 3-й пункт алгоритма. Для начала, решим задачу (7), (12) с помощью табличного процессора MicrosoftExcel (см. Приложение 2) и получим X₂ = (2; 1)[2] , z₂ = 10 (14). Так как z₂ ≥ z₀ , «оптимальным» становится план Х₀ .

Решим задачу (7), (13). Из последнего уравнения очевидно, что x₂ = 0. Отсюда следует, что x₁ = 3 (максимально возможное). Тогда Х₃ = (3; 0), z₃ = 13 (15), а следовательно, данный план является оптимальным (теперь уже без кавычек).

Нам не пришлось выполнять 4-й пункт нашего алгоритма в связи с тем, что оптимальное решение найдено, переменные целочисленные. К тому же, все необходимые моменты решения уже были показаны в пунктах 1-3.

Пример, в котором всё складывается не так просто, приведен в Приложении 3.

календарное планирование программирование

III. Применение метода ветвей и границ для задач календарного планирования

Метод ветвей и границ является универсальным методом решения комбинаторных задач дискретного программирования. Сложность практического применения метода заключается в трудностях нахождения способа ветвления множества на подмножества и вычисления соответствующих оценок, которые зависят от специфики конкретной задачи.

Для того, чтобы выяснить области применения данного метода и ознакомиться с практической его формой, мы обратимся к задаче трех станков[3] , как к классическому примеру.

§1. Алгоритм решения задачи трех станков методом ветвей и границ

Заданыnдеталей d_i (i= 1, 2, ..., n), последовательно обрабатываемых на трех станках R₁ , R₂ , R₃ , причем технологические маршруты всех деталей одинаковы. Обозначим a_i ,b_i ,c_i — длительность обработки деталей d_i на первом, втором и третьем станках соответственно.

Определить такую очередность запуска деталей в обработку, при которой минимизируется суммарное время завершения всех работ T_ц .

Можно показать, что в задаче трех станков очередность выполнения первых, вторых и третьих операций в оптимальном решении может быть одинаковой (для четырех станков это свойство уже не выполняется). Поэтому достаточно определить очередность запуска только на одном станке (например, третьем).

Обозначимs_k = (i₁ , i₂ , ..., i_k ) — некоторую последовательность очередности запуска длиной k(1 £k£n) и A(s_k ), В (s_k ), С (s_k ) — время окончания обработки последовательности деталей s_k на первом, втором и третьем станках соответственно.

Необходимо найти такую последовательность s_опт , что

С(s_опт ) = min С (s). (16)

§1.1 Реккурентное вычисление A( s_k ), В(s_k ), C(s_k ) и условие доминирования

Покажем, как можно рекуррентно вычислять A(s_k ), В (s_k ), С (s_k ). Пусть s_{k +1} = (s_k ,i_{k + i} ), т. е. последовательность деталей s_{k +1} получена из деталей s_k с добавлением еще одной детали i_{k +1} . Тогда:

A (s_k+1 ) = A (s_k )+ (17),

В (s_{k +1} ) = max [A(s_{k +1} ); В (s_k )] + (18),

С (s_{k +1} ) = max [В (s_{k +1} ); С (s_k )] + (19).

Логика выражений (17) – (19) очевидна, особенно если рассмотреть задачу двух станков.

Для задачи трех станков можно использовать следующее правило доминирования:

Если s — некоторая начальная последовательность, а — подпоследовательность, образованная из s перестановкой некоторых символов, то вариант s доминирует над , когда выполняются следующие неравенства:

А (s) £ А (), В (s) £ В (), С (s) £ С () (20),

причем хотя бы одно из них выполняется как строгое неравенство.

§1.2 Способ конструирования вариантов последовательностей s и вычисления оценок D(s) для каждого из них

Способ конструирования вариантов последовательностей s и вычисления оценок D(s) для каждого из них состоит в следующем:

Пусть имеется начальная подпоследовательность s. Тогда вычисляются величины:

d_C (s) = С(s) +, (21)