Курсовая работа: Применение метода ветвей и границ для задач календарного планирования

z^* =13,5,Х₁ ^* =(3;0,5;0;1;0;2,5).

Приложение 2

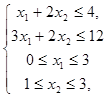
Решение задачи z = 4х₁ + х₂ +1 ® max при ограничениях:

с помощью табличного процессора MicrosoftExcel.

Приложение 3

В качестве примера применения метода ветвей и границ приведем поиск оптимального значения функции Z = Зх₁ + х₂ ® max при ограничениях:

4x_l + Зх₂ < 18,

x₁ + 2x₂ £ 6,

0 £x₁ £ 5,

0 £x₂ £ 4,

х₁ , x₂ — целые числа.

Решение

За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т.е. Z₀ = Z (0; 0) = 0.

I этап. Решая задачу симплекс-методом, получим Z_max = 13,5 при Х₁ ^* = (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента х₁ ^* дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение х₁ ^* , т.е. 4 < х₁ < 5. Поэтому задача 1 разбивается на две задачи 2 и 3.

Задача 2

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

0 £x₁ £ 4

0 £x₂ £ 4

х₁ , x₂ — целые числа.

Задача 3

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6