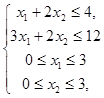Курсовая работа: Применение метода ветвей и границ для задач календарного планирования

∆ (s = 0) = max {17, 17,14} = 17.

2 ) Первый шаг. Конструируем все возможные последовательности длиной 1

s₁ ⁽¹⁾ = 1; s₂ ⁽¹⁾ = 2; s₃ ⁽¹⁾ = 3; s₄ ⁽¹⁾ = 4; s₅ ⁽¹⁾ = 5.

Находим:

d_A ⁽¹⁾ = A₁ + + = 14 + 3 = 17;

d_B ⁽¹⁾ = В₁ + + = 5 + 12 + 2 = 19;

d_C ⁽¹⁾ = С₁ + = 9 + 10 = 19 .

Откуда ∆ (1) = max {17, 19, 19} = 19.

Аналогично определяем ∆ (2), ∆ (3), ∆ (4), ∆ (5).

3) Второй шаг. Среди множества подпоследовательностей длиной 1, s₁ ⁽¹⁾ = 1, s₂ ⁽¹⁾ = 2,..., s₅ ⁽¹⁾ = 5 выбираем наиболее перспективную s = 1, для которой величина оценки-прогноза ∆ (s) оказывается наименьшей. Далее развиваем ее, конструируя возможные варианты длиной 2, т. е. (1.2), (1.3), (1.4), (1.5).

Для каждого из этих вариантов вновь определяем оценки по формулам (21) — (24).

Процесс вычислений продолжаем аналогично.

Процесс построения дерева вариантов приведен на рис. 1.

Рисунок 1

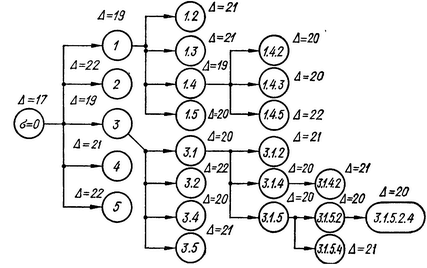
Каждой конечной вершине дерева вариантов будет отвечать полная последовательность s = i₁ ,i_2, ,.i_n . Если для некоторой такой вершины величина оценки ∆ (s) не превосходит величины оценок для всех остальных вершин, то эта оценка определяет искомый оптимальный вариант. В противном случае разбиваем более перспективный вариант с наилучшей оценкой.

Конечная вершина определяет вариант (последовательность) = 3, 1, 5, 2, 4 с наилучшей оценкой ∆ = 20. Поэтому данный вариант является оптимальным.

Непосредственной проверкой убеждаемся, что время обработки всей последовательности деталей для этого варианта совпадает со значением оценки-прогноза и является минимальным:

.

Список литературы

1. Акулич И.Л. Математическое программирование в примерах и задачах. М., Высшая школа, 1993.

2. Гончаренко В.М. «Математические методы и модели операций. Руководство к решению задач». М., Финансовая Академия, 2006.

3. Зайченко Ю.П. Исследование операций. Киев, Высшая школа, 1975.

4. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М., Высшая школа, 1980.

5. Шкурба В.В. Задача трех станков. М., Наука, 1976.

Приложение 1

Решение задачи

z = 4х₁ + х₂ +1 ® max при ограничениях: