Курсовая работа: Применение методов дискретной математики в экономике
Заданием в данном пункте является построение таблицы истинности для следующего высказывания:
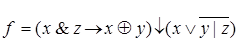 ,
,
Высказыванием называется повествовательное предложение, о котором можно сказать в данный момент, что оно истинно или ложно, но не то и другое одновременно. “Истинность” или “ложность” предложения – это истинностное значение высказывания. Каждому высказыванию сопоставляется переменная, равная 1, если высказывание истинно, и равная 0, если оно ложно. Эти высказывания будут считаться простыми. Из простых высказываний с помощью логических связок могут быть построены составные высказывания. В таблице 1 приведены некоторые логические связки, используемые при задании данной функции (1).
Таблица 1-Логические связки
| Название | Обозначение |
| Конъюнкция | & |
| Импликация | ® |
| Сумма по модулю два | Å |
| Штрих Шеффера | | |
| Отрицание | Ø |
| Дизъюнкция | Ú |
| Стрелка Пирса | ¯ |
Правильно построенные составные высказывания называются (пропозиционарными) формулами. Истинностное значение формулы определяется через истинностные значения её составляющих в соответствии с единой таблицей истинности (таблица 2).
Таблица 2-Истиностные значения формул высказывания
| Х1 | Х2 | X1 &X2 | X1 ® X2 | X1 ÅX2 | X1 Ú X2 | ØX1 | X1 ¯ X2 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Для того чтобы составить таблицу истинности для формулы, необходимо выполнить последовательность всех логических операций.
![]() , (1)
, (1)
После последовательного выполнения всех логических операций составляется таблица истинности для данной функции
Таблица 3- Таблица истинности функции (1)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | y | z | & | ||||||
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
Приведение функции к конъюнктивным и дизъюнктивным нормальным формам. Конъюнктивным (дизъюнктивным) одночленом от переменных а1 , а2 , а3 ,…,а n называется конъюнкция (дизъюнкция) этих переменных или их отрицаний. Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных произведений (конъюнктивных одночленов), называется дизъюнктивной нормальной формой (ДНФ) данной формулы. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных произведений (дизъюнктивных одночленов), называется конъюнктивной нормальной формой (КНФ) данной формулы /2/. Справедливы следующие теоремы: любая булева функция, тождественно не равная нулю, представима и притом единственным образом в виде ДНФ по формуле:
![]() V
V![]() (2)
(2)
Любая булева функция, тождественно не равная единице представима и притом единственным образом в виде КНФ.
![]() L
L![]() (3).
(3).
Любая булева функция представима формулой, в которую входит только конъюнкция, дизъюнкция и отрицание /2/.
Искомая ДНФ для функции (1) имеет вид:
![]()
Искомая КНФ для функции (1) будет иметь следующий вид:
![]()
В расчетах ДНФ и КНФ использована методика /2/.
Построение полинома Жегалкина.
Представление булевой функции над базисом {0,1,v,Å} называется полиномом Жегалкина.
Таким образом, всякая булева функция представима в виде:
![]()
![]()
где ∑ - сложение по модулю два, знак · обозначает конъюнкцию/7/.
Для функции f ( x , y , z ) (1) полином Жегалкина имеет вид:
P(x, y, z)=b0 ×1Åb1 ×xÅb2 ×yÅb3 ×zÅb4 ×x×yÅb5 ×x×zÅb6 y×zÅb7 x×y×z
Метод неопределенных коэффициентов заключается в том, что путем последовательной подстановки переменных x, y, z и соответственно значений функции при этих переменных, из таблицы 1 в данный полином (4), строится система уравнений:
![]() 0=b0 ×1Åb1 ×0Åb2 ×0Åb3 ×0Åb4 ×0×0Åb5 ×0×0Åb6 0×0Åb7 0×0×0
0=b0 ×1Åb1 ×0Åb2 ×0Åb3 ×0Åb4 ×0×0Åb5 ×0×0Åb6 0×0Åb7 0×0×0