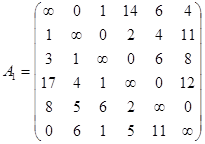Курсовая работа: Применение методов дискретной математики в экономике
Рисунок 2 – Решение задачи о оптимальной структуре сети
Коммуникации проложат между следующими пунктами: аптека – кафе - завод №2 – магазин №1 - завод №1 – хлебозавод – магазин №2 - продуктовый магазин – обувная фабрика – магазин №3 – торговый центр.
2.2 Применение алгоритма Дейкстры
Фирме, занимающейся перевозкой скоропортящихся товаров, необходимо доставить товар из Суйфэньхе в Хабаровск, причем маршрутов, по которым можно произвести доставку несколько. Расстояние между Суйфэньхе и городом 2 составляет 15 км, между Суйфэньхе и городом 3 – 20 км, между Суйфэньхе и городом 11 – 85 км. Между городом 2 и городом 4 - 25 км, между городом 2 и городом 7 - 65 км. Между городом 3 и городом 5 составляет 5 км, между городом 3 и городом 8 - 50 км. Между городом 4 и городом 8 - 20 км. Между городом 5 и городом 6 - 20 км. Между городом 6 и городом 7 - 25 км, между городом 6 и городом 8 - 35 км. Между городом 7 и городом 9 - 15 км, между городом 7 и городом 10 - 40 км. Между городом 9 и городом 12 - 20 км. Между городом 10 и городом 11 - 30 км, между городом 10 и городом 12 - 45 км. Между городом 11 и городом 12 - 25 км. Требуется найти кратчайший путь из Суйфэньхе в Хабаровск
Строится граф G, в котором город Суйфэньхе обозначается цифрой 1, Хабаровск - 12. Остальные пункты маршрута обозначаются цифрами 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. Каждому ребру графа сопоставляется число, которое будет равняться расстоянию между пунктами. Требуется найти минимальный маршрут. Алгоритм Дейкстры находит кратчайший путь между двумя вершинами в графе /3/. Следовательно, можно воспользоваться им, при решении данной экономической задачи.
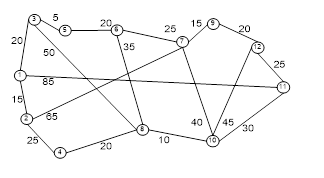
Рисунок 3– Графическая интерпретация задачи о нахождении минимального маршрута доставки
Если вершина v лежит на кратчайшем пути от начальной вершины к конечной, то T[v] – длина кратчайшего пути от начальной вершины к конечной.
![]()
С помощью алгоритма Дейкстры находится единственный минимальный маршрут, соединяющий вершины 1и 12 графа G (рисунок 3).
Пусть вершина – номер 1 – начальная вершина. Для неё назначается постоянный ярлык L(к) = 0. Конечной вершиной будет считаться вершина номер 1. Рассматриваются вершины, смежные с вершиной 12, и назначим им временные ярлыки: L(2) = 25 , L(3) = 20 , L(11) = 85.
Нужно выбирать вершину с самым маленьким ярлыком – это вершина номер 3, и её ярлык L(3) = 20 становится постоянным.
Повторяя этот процесс для вершины номер 3, вершинам присваиваются временные ярлыки: L(5) = 5 , L(8) = 50.
Среди всех временных ярлыков минимальный будет у L(5) = 5. Этот ярлык становится постоянным.
С вершиной 5 смежна только вершина 6. L(6) = 20.
Повторяя этот процесс для вершины номер 6, вершинам присваиваются временные ярлыки: L(7) = 25 , L(8) = 35.
Среди всех временных ярлыков минимальный будет у L(7) = 25. Этот ярлык становится постоянным.
Повторяя процесс, рассматриваются вершины, смежные с вершиной 7. Это 2, 9 и 10. Для которых временные ярлыки будут: L(2) = 65, L(9) = 15, L(10) = 40. Находится наименьший временный ярлык. Он будет у: L(9) = 20.
С вершиной 9 смежна только вершина 12. L(12) = 20.
Теперь, когда дерево сформировано, мы можем определить самый короткий путь от 1 до 12. Этот путь дерева, соединяющий вершины 1 и 12. И он проходит через вершины 3, 5, 6, 7 и 9. Длина этого пути - L(v') = 20 + 5 + + 20 + 25 + 15 + 20 = 105 (км.).
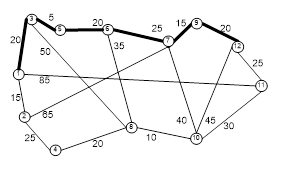
Рисунок 4 - Решение задачи о нахождении минимального маршрута доставки
Маршрут из города Суйфэньхе в Хабаровск, при котором время доставки товара будет наименьшим, включает город 3, город 5, город 6, город 7 и город 9.Длина маршрута составит 105 километров.
2.3 Задача коммивояжера
Коммивояжер желает посетить 6 городов. Они соединены сетью дорог
Расстояние между городом 1 и городом 2 составляет 6 км, между городом 1 и городом 3 - 7 км, между городом 1 и городом 4 - 20 км, между городом 1 и городом 5 - 12 км, между городом 1 и городом 6 - 10 км. Расстояние между городом 2 и городом 3 составляет 5 км, между городом 2 и городом 4 - 7 км, между городом 2 и городом 5 - 9 км, между городом 2 и городом 6 - 16 км. Расстояние между городом 3 и городом 4 составляет 4 км, между городом 3 и городом 5 - 10 км, между городом 3 и городом 6 - 12 км. Расстояние между городом 4 и городом 5 составляет 3 км, между городом 4 и городом 6 - 15 км. Расстояние между городом 5 и городом 4 составляет 6 км, между городом 5 и городом 6 - 4 км, между городом 6 и городом 3 - 11 км, между городом 6 и городом 5 - 21 км. Коммивояжёр должен посетить все 6 городов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным
Данную задачу можно решить венгерским методом, методом совершенного паросочетания. Для этого требуется построить матрицу А, отображающую длину между городами: aij – расстояние от города i до городаj (i ≠j ), если i = j , то ставится ∞ ,так как дороги не существует.
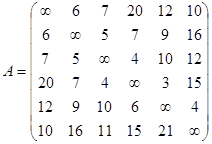
Строится приведенная матрица с целью получения в каждой строке и столбце не меньше одного кратчайшего маршрута (нулевого приведенного значения). Для этого в каждой строке матрицы А от каждого элемента отнимается значение минимального элемента этой строки: