Курсовая работа: Применение методов математической статистики и теории вероятностей в задачах теоретической лингвистики при анализе устной и звучащей речи на русском и английском языках

Очевидно то, что в стихотворении Вильяма Блейка вероятность появления гласных звуков превышает соответствующую вероятность в стихотворении Зинаиды Гиппиус, поэтому можно с полной уверенностью утверждать, что произведение «TheCradleSong» названо автором как нельзя кстати – «колыбельная» - певучая, плавная, спокойная.

2.9 Коэффициент темпа речи

T =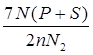

Гдеn – количество знаменательных слов,

Р – количество подлежащих,

S – количество сказуемых,

N – количество простых предложений,

N – количество двусоставных предложений.

Для «Свободного стихотворения»:

T = = 9.33

Для «Колыбельной»:

T = 1.23

Темп речи первого стихотворения значительно превышает соответствующий показатель во втором, отсюда следует, что второе стихотворение более спокойное, плавное, что снова подтверждает, что Вильям Блейк отлично подобрал название для своего творения.

3. Объединённый коэффициент синтаксической и ритмомелодической сложности

Так как предметами моего исследования являются два стихотворения, то формула для расчета объединённого коэффициента синтаксической и ритмомелодической сложности может сыграть огромную роль в изучении данных текстов с точки зрения устной и звучащей речи и выявлении разницы между ними.

Общая формула выглядит следующим образом:

Сл =

Где n – количество знаменательных слов,

T- количество безударных слогов,

l – количество строк,

N =105, как нам известно из предыдущих исследований.

Сл1.0762

Сл0.314

Из данных подсчётов можно сделать вывод, что стихотворение воспринимается на слух сложнее, чем стихотворение Вильяма Блейка.

4. Вывод

Рассмотренное исследование наглядно иллюстрирует возможности методов математической статистики и теории вероятностей в задачах математической лингвистики. Там, где одной только интуиции читателя недостаточно, так как она всегда субъективна и недостаточно достоверна, применяется математический подход – строгий, объективный, основывающийся на математической модели стиля определенного вида. В моём примере была рассмотрена вероятностная модель текста – наиболее распространённая для решения сложных задач лингвистического анализа, но отнюдь не единственная.

Сравнив «Свободное стихотворение» Зинаиды Гиппиус и «TheCradleSong» Вильяма Блейка с помощью методов математической статистики и теории вероятностей, я пришла к выводу, что стиль Зинаиды Гиппиус более разнообразный, сложный, непредсказуемый, а стихотворение английского поэта – более плавное, спокойное, певучее, мелодичное, легко воспринимающееся на слух.

5. Список литературы

1. Р.Г. Пиотровский, К.Б. Бектаев, А.А. Пиотровская, Математическая Лингвистика, - М.: Высшая школа, 1977

2. В.В. Савченко, Теория вероятностей и математическая статистика: Конспект лекций, - Н. Новгород: НГЛУ, 2003

3. В.В. Савченко, В. В. Ретивина, Математика и информатика для лингвистов, краткий конспект лекций, - Н. Новгород: НГЛУ, 2006

4. ВВ Власов, Конспект лекций по высшей математике, - М.: Айрис, 1997

5. Р.Г. Пиотровский, К.Б. Бектаев, Математические методы в языкознании. Часть 2. математическая статистика и моделирование текста, Алма-ата: КазГУ, 1973