Курсовая работа: Применение уравнение Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы

Подставляя найденные значения обеих сумм в равенство (7) и рассматриваем механическую систему со стационарными идеальными связями, для которых :

+,

или

=(j = 1,2,…, s). (10)

Систему s дифференциальных уравнений (10) называют уравнениями Лагранжа второго рода. Эти уравнения представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат системы .Интегрируя эти дифференциальные уравнения и определяя по начальным условиям постоянные интегрирования, получаем s уравнений движения механической системы в обобщенных координатах:

(j=1, 2,…, s).

6 Уравнения второго рода для консервативной системы

Предположим, что на рассматриваемую механическую систему наряду с силами, имеющими потенциал (консервативными силами), действуют силы, не имеющие потенциала (неконсервативные силы). При этом условии обобщенную силу удобно представить в виде суммы обобщенной силы , соответствующей консервативным силам , и обобщенной силы , соответствующей неконсервативным силам :

=+.

Если на рассматриваемую систему действуют только консервативные силы, то обобщенная сила определяется формулой:

= = (j=1,2,…, s).

В этом случае уравнения Лагранжа второго рода принимают следующий вид:

= (j = 1,2,…, s). (11)

Уравнения (12) можно преобразовать путем введения функции Лагранжа L = Т – П, называемой кинетическим потенциалом.

П = П (t).

Следовательно, кинетический потенциал L является функцией обобщенных координат, обобщенных скоростей и времени:

Потенциальная энергия является функцией только обобщенных координат и времени, а потому

(j=1,2,…, s).

Пользуясь этим условием, получим

,

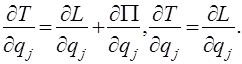
Подставим эти частные производные в уравнения Лагранжа (11):

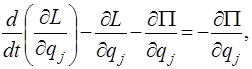
или

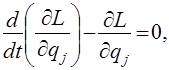(j=1,2,…, s). (12)

Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы.

7 Применение уравнений Лагранжа II рода к исследованию движения механической системы