Курсовая работа: Применение уравнение Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы

Для определения постоянных и , используя начальные условия: при t=0 x=0; x=0.

Из (19) и (20) следует =0 и =0.

Тогда

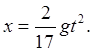(21)

Уравнение (21) является уравнением движения системы, описывающим изменение первой обобщенной координаты.

Чтобы получить второе уравнение движения, находим из (17)

(22)

Интегрируя (23), получаем

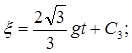(23)

(24)

Для определения постоянных и , используя начальные условия: при t=0 =0;=0.

Из (24) и (25) следует =0 и =0.

Тогда

(25)

Уравнение (25) является уравнением движения системы, описывающим изменение второй обобщенной координаты.

Заключение

Итак, уравнения Лагранжа II рода применяются для исследования движения механической системы с двумя степенями свободы. Чтобы для данной механической системы составить уравнения Лагранжа, необходимо установить число степеней свободы системы и выбрать обобщённые координаты; изобразить систему в произвольном положении и показать все действующие силы; вычислить обобщённые силы; определить кинетическую энергию системы в её абсолютном движении и выразить её через обобщённые скорости; составить уравнения Лагранжа.

Уравнения Лагранжа дают единый метод решения задач динамики, они не зависят от числа и количества точек, входящих в рассматриваемую систему, от движения самой системы. Уравнения Лагранжа представляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщённых координат. Число уравнений Лагранжа определяется только числом степеней свободы системы.

Список использованной литературы

1. С.М. Тарг «Краткий курс теоретической механики» – М.: Высшая школа, 1986 г., 416.

2. А.А. Яблонский «Курс теоретической механики» – М.: Высшая школа, 1984 г., 436.