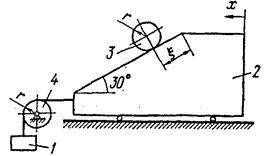
Курсовая работа: Применение уравнение Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы
Массы тел механической системы m![]() = 2m; m
= 2m; m![]() = 6m; m
= 6m; m![]() =m. Начальные условия:
=m. Начальные условия:![]() ,
,![]() ,
,![]() ,
,![]() .
.
Найти уравнения движения системы в обобщенных координатах ![]() ,
,![]() .
.
Для решения задачи применим уравнения Лагранжа II рода:
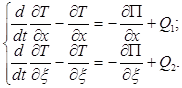
![]() (13)
(13)
Здесь T – кинематическая энергия; ![]() – потенциальная энергия;
– потенциальная энергия; ![]() и
и![]() – обобщенные силы, соответствующие неконсервативным силам.
– обобщенные силы, соответствующие неконсервативным силам.
Для данной системы  (14)
(14)
Введем переменную ![]()
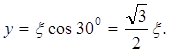
Выразим скорости центров масс твердых тел системы через обобщенные скорости:
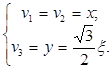
Угловая скорость тела 4 ![]()
Момент инерции тела 4 ![]()
Кинематическая энергия тел 1 – 4:
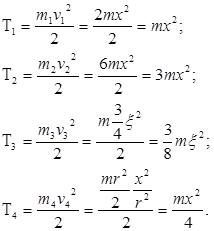
Подставляя эти величины в (14), получим
![]()
![]() +
+![]() +
+![]() +
+![]() =
=![]()
Тогда
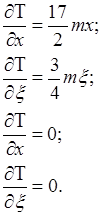 (15)
(15)
Потенциальную энергию системы находим как работу сил тяжести твердых тел 1 и 3 при их перемещении из данного положения, характеризуемого координатами x и ![]() , в некоторое исходное нулевое, например то, от которого ведется отсчет обобщенных координат:
, в некоторое исходное нулевое, например то, от которого ведется отсчет обобщенных координат:
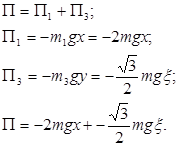
Тогда
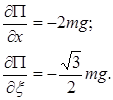 (16)
(16)
Обобщенные силы ![]() = 0 и
= 0 и ![]() =0 (т. к. на механическую систему не действуют силы
=0 (т. к. на механическую систему не действуют силы ![]() ).
).
Подставляя (15) и (16) в (13), получаем дифференциальные уравнения движения системы:
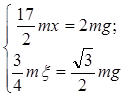 (17)
(17)
Выражая x из (18), получаем
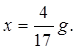 (18)
(18)
Интегрируя (19), получаем
![]() (19)
(19)