Курсовая работа: Принятие решений в условиях риска 3

представляющую собой наименьший выигрыш игрока А при состоянии природы П _j . Тогда имеем:

r_ij ≤ β _j - ω _j , i= 1, …, m ; j =1, …, n. (5)

Разность β _j - ω _j естественно назвать колебанием выигрышей при состоянии природы П _j , j = l, ..., п

Если a_ij = β _j , то r_ij = 0, т.е. стратегия А _i при состоянии природы П _j является безрисковой.

Если a_ij = ω _j , то риск r_ij , является максимальным. Следовательно, по критерию риска стратегия А _i в этом случае наихудшая.

Если β _j = ω _j , то все выигрыши j -столбце матрицы игры равны между собой: ω _j = a _{1 j} = a _{2 j} = … = a_mj = β _j и риск r_ij = 0. Поэтому в этом случае любая стратегия игрока А при состоянии природы П _j безрисковая.

Для матрицы А матрица рисков R_A имеет ту же размерность и следующий вид:

Таблица 2 – Матрица рисков

RA =	П j А i	П 1	П 2	…	П n
	А1	r11	r12	…	r1n
	А2	r21	r22	…	r2n
	…	…	…	…	…
	А m	rm1	rm2	…	rmn

Отметим, что матрица выигрышей А однозначно порождает матрицу рисков R_A , поскольку каждый риск r_ij однозначно определяется соответствующими показателем благоприятности β _j состояния природы П _j , и выигрышем a_ij . Обратное неверно: одна и та же матрица рисков может соответствовать разным матрицам выигрышей.

В понятии оптимальной стратегии лежат различные соображения, составляющие содержание соответствующих критериев оптимальности стратегий.

Перед тем как переходить к выбору оптимальной стратегии, целесообразно возможности упростить матрицу А, уменьшив число строк на основании принципа доминирования стратегий игрока А.

1.2 Упрощение матрицы игры

Если какая-нибудь из стратегий игрока А окажется доминирующей каждую из остальных его стратегий, то она и должна выбираться игроком А в качестве пред­почтительной, поскольку его выигрыш при этой стратегии и при любом состоянии природы П не меньше выигрыша при любой из остальных стратегий.

Если же матрица игры не обладает указанным свойством, т.е. у игрока А нет стратегии, доминирующей каждую из остальных его стратегий, то нужно посмотреть, нет ли у него доминируемых или дублирующих стратегий. При наличии таковых, соответствующие им строки матрицы можно удалить, уменьшив тем самым ее размерность.

Таким образом, в играх с природой можно и полезно пользоваться принципом доминирования стратегий игрока А (строк матрицы игры). Однако принцип до­минирования стратегий (состояний) природы (столбцов матрицы игры) недопустим, поскольку природа не выбирает свои состояния с целью по возможности большего уменьшения выигрышей игрока А, для нее нет более или менее эффективных состояний.

1.3 Критерий Байеса относительно выигрышей

Предположим, что статистик из прошлого опыта известны не только состояния П _j , j = l, ..., п , в которых может находиться природа П , но и соответствующие вероятности q₁ , ..., q_n с которым природа П реализует эти состояния. Тогда мы находимся в ситуации принятия решения в условиях риска.

Показателем эффективности стратегии А_i по критерию Байеса относительно выигрышей называется среднее значение, или математическое ожидание выигрыша i-й строки с учетом вероятностей всех возможных состояний природы. Обозначая это среднее значение через ā _i , будем иметь:

ā _i = q₁ a_{i 1} + q₂ a_{i 2} + … + q_n a_in = 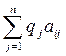, i = 1, …, m . (6)

Таким образом, a_t представляет собой взвешенное среднее выигрышей i-й строки, взятых с весами q₁ , ..., q_n .

Оптимальной среди чистых стратегий по критерию Байеса относительно выигрышей считается стратегия А_{i 0} с максимальным показателем эффективности, т.е. с максимальным средним выигрышем:

ā_i0 = max ā_i . (7)

^{1≤ i ≤m}

Таким образом, выбранное решение по этому критерию является оптимальным не в каждом отдельном случае, а в среднем.

Распространим понятие показателя эффективности по критерию Байеса относительно выигрышей на смешанные стратегии игрока П .

Пусть P = ( p₁ , ..., p_n ) - некоторая смешанная стратегия игрока А, при которой чистая стратегия А_i используется им с вероятностью p_i , i =1, ..., т. Тогда выигрыш игрока А при смешанной стратегии P = ( p₁ , ..., p_n ) и при состоянии природы П _j будет равен

H (P , П _j ) = 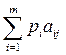, j =1, …, n. (8)

Показателем эффективности смешанной стратегии P = ( p₁ , ..., p_n ) по критерию Байеса относительно выигрышей назовем среднее значение выигрышей, с учетом вероятностей q₁ , ..., q_n состояний природы. Обозначим этот показатель через .

Получим:

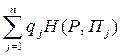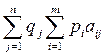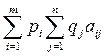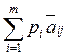= = = = . (9)