Курсовая работа: Принятие решений в условиях риска 3

Если, в частности, стратегия P = ( p₁ , ..., p_n ) является чистой стратегией А _k , k = l, ..., m , то p_i = 0 i ≠ k, p_k = 1, и ее показатель эффективности как смешанной стратегии , превращается в ее показатель эффективности как чистой стратегии ā _k , вычисляемый по формуле (6).

Пусть S_A - множество всех смешанных (в том числе и чистых) стратегий игрока A. Оптимальной среди всех стратегий множества S_A по критерию Байеса относительно выигрышей назовем стратегию P ⁰ , показатель эффективности (9) которой максимален:

max =. (10)

^{P ϵ S a}

Стратегия А _{i 0} оптимальная среди чистых стратегий по крите­рию Байеса относительно выигрышей, является оптимальной по тому же критерию и среди всех смешанных стратегий множества S_A .

При принятии решений в условиях риска по критерию Байеса относительно выигрышей можно обойтись только чистыми стратегиями, не используя смешанные.

1.4 Критерий Байеса относительно рисков

Рассмотрим ту же игру с природой матрицей, в которой известны вероятности состояний природы q₁ , ..., q_n . При принятии решений в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы A , используя формулу рисков (3)

Таблица 3 – Матрица рисков

П j А i	П 1	П 2	…	П n
А1	r11	r12	…	r1n
А2	r21	r22	…	r2n
…	…	…	…	…
А m	rm1	rm2	…	rmn

Показателем неэффективности стратегии А _i по критерию Байеса относи­тельно рисков называется среднее значение, или математическое ожидание риска i-й строки матрицы (таблица 3), вероятности которых, очевидно, совпадают с вероятностями состояний природы. Обозначим средний риск при стратегии А _i через ṝ_i , тогда

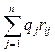ṝ_i = q₁ r_i1 + q₂ r_i2 + … + q_n r_in = , i= 1, …, m. (11)

является взвешенной средней рисков i -й строки матрицы (таблица 3) с весами p_i , i =1, ..., т.

Оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия П _j , показатель неэффективности (11) которой минимален, т.е. минимален средний риск

ṝ_i0 = min ṝ_i . (12)

^{1≤ i ≤ m}

Определим понятие риска при использовании игроком А смешанной стратегии и при состоянии природы П _j , j = l, ..., п , как разность

r (P , П _j ) = [max H (U , П _j )] - H (P , П _j ), j =1, …, n. (13)

^{U ϵ S a}

между максимальным выигрышем max H (U , П _j ) при всех смешанных стратегиях U = ( u₁ , ..., u_n ) ϵ S_A и при состоянии природы П _j и выигрышем H (P , П _j ) при смешанной стратегии P = ( p₁ , ..., p_n ) и при состоянии природы П _j .

В качестве показателя неэффективности смешанной стратегии P = ( p₁ , ..., p_n ) по критерию Байеса относительно рисков рассмотрим взвешенную среднюю рисков (13) с весовыми коэффициентами, равными вероятностям q₁ , ..., q_n состояний природы:

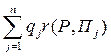= . (14)

Оптимальной среди всех смешанных (в том числе и чистых) стратегий по критерию Байеса относительно рисков будем считать стратегию P ⁰ , показатель неэффективности которой, вычисляемый по формуле (14), минимален:

min =. (15)

^{P ϵ S a}

Если А _{i 0} - стратегия, оптимальная среди чистых стратегий по критерию Байеса относительно рисков, то она является оптимальной по тому же критерию и среди всех смешанных стратегий множества S_A .

При принятии решения в условиях риска по критерию Байеса относительно рисков так же как и в случае критерия Байеса относительно выигрышей достаточно использовать одни чистые стратегии, не рас­сматривая смешанные.

Критерии Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия А _{i 0} является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот, стратегия А _{i 0} , оптимальная по критерию Байеса относительно рисков, оптимальна и по критерию Байеса относительно выигрышей.

1.5 Критерий Лапласа относительно выигрышей

В предыдущих двух критериях Байеса известные вероятности q₁ , ..., q_n состояний природы могли быть получены из статистических данных, отражающих многократное решение подобных задач, или в результате наблюдений за поведением природы. Однако, довольно часто складывается такая ситуация, когда мы лишены возможности определить вероятности состояний природы указанными способами. Желая все же принять решение в условиях риска, мы вынуждены оценить вероятности состояний природы субъективно. Существуют различные методы численной субъективной оценки степени правдоподобности состояний природы. Один из них состоит в том, что мы не можем отдать предпочтение ни одному из состояний природы, и потому считаем их равновероятными, т.е. q₁ = .. .=q_n = . Этот принцип называется «принципом не­достаточного основания» Лапласа. На нем основан критерий Лапласа относительно выигрышей.

Показателем эффективности стратегии А _i по критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышей i -й строки:

ā _i = 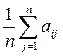, i = 1, …, m . (16)