орой, вычисляемый по формуле (16), максимален, т.е. ā _{i 0} = max ā _i .

^{1≤ i ≤ m}

Очевидно, что критерий Лапласа относительно выигрышей есть частный случай критерия Байеса относительно выигрышей при q₁ = .. .=q_n = . Поэтому все ут­верждения на счет критерия Байеса относительно выигрышей, остаются в силе и для критерия Лапласа относительно выигрышей.

Подставляя (16) в (9), получим показатель эффективности смешанной стратегии P = ( p₁ , ..., p_n ) по критерию Лапласа относительно выигрышей

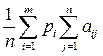= . (17)

Стратегия P = ( p₁ , ..., p_n ) будет оптимальной среди всех смешанных стратегий множества S_A по критерию Лапласа относительно выигрышей, если она максимизирует показатель эффективности (17).

Оптимальная среди чистых стратегия А _i по критерию Лапласа относительно выигрышей является оптимальной по тому же критерию и среди всех смешанных стратегий.

1.6 Критерий Лапласа относительно рисков

Критерий Байеса относительно рисков при равновероятных состояниях природы, q₁ = .. .=q_n = , превращается в критерий Лапласа относительно рисков. Тогда величина 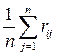, получающаяся из (11) при q_j = , j =1, …, n , или более простая величина представляет собой показатель неэффективности стратегии А _i по критерию Лапласа относительно рисков. Следовательно, оптимальной среди чистых стратегий по критерию Лапласа относительно рисков является стратегия А _{i 0} , показатель неэффективности 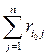которой минимален. Подставляя в (14) значения q_j = , j =1, …, n , получим показатель неэффективности смешанной стратегии Р по критерию Лапласа относительно рисков, вместо которого можно рассматривать более простую величину = 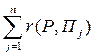. Стратегия Р, для которой показатель принимает минимальное значение, является оптимальной среди всех стратегий множества S_A . Чистая стратегия, оптимальная среди чистых стратегий по критерию Лапласа относительно рисков, оптимальна по тому же критерию и среди всех смешанных стратегий множества S_A .

Критерии Лапласа относительно выигрышей и относительно рисков эквивалентны.

1.7 Критерий относительных значений вероятностей состояний природы с учетом выигрышей (рисков)

В практике принятия решений часто встречается случай, когда нам неизвестны вероятности состояний природы, но мы имеем представление о том, какие состояния природы более правдоподобны, какие менее правдоподобны, а какие равноправдоподобны. Поэтому мы можем расположить (неизвестные) вероятности состояний природы в виде убывающей или возрастающей последовательности. Для простоты предположим, что расположение q₁ , ..., q_n уже и есть монотонная последовательность. Если, например, эта последовательность строго убывает, то правдоподобнее всех состояние П₁ затем по степени правдоподобности следует состояние П₂ , и т. д., наименьшей правдоподобностью обладает состояние П _n . Не зная, на сколько одна вероятность состояния природы отличается от другой, мы можем предположительно придать им относительные значения, пропорциональные членам некоторой (подходящей на наш взгляд) монотонной последовательности положительных чисел τ ₁ , ..., τ _n , т.е.

q₁ : q₂ : q₃ : ... : q_n = τ ₁ : τ ₂ : τ ₃ : ... : τ _n . (18)

Из (18) следует, что если q₁ , ..., q_n убывающая, соответственно возрастаю­щая, последовательность, то убывающей, соответственно возрастающей, является и последовательность τ ₁ , ..., τ _n .

При этом следует учитывать нормировочное равенство

=1 (19)

Вероятность j -ого столбца определяется по формуле:

q_j = , j =1, …, n (20)

Из (20) и (19) получим:

1 = = = 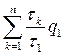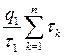. (21)

Из (21) выразим q₁ вероятность возникновения состояния природы П₁ :

q₁ = 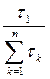. (21)

Тогда:

q_j = . (22)

Мы нашли значения вероятностей q_j , j =1, …, n , состояний природы.

Критерий Байеса относительно выигрышей при вероятностях состояний природы назовем критерием относительных значений вероятностей состояний природы с учетом выигрышей. При этом критерии показателем эффективности стратегии А _i является величина ā _i , получающаяся из равенства (6) подстановкой в него вероятностей (22):

ā _i =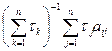, i =1, …, m . (23)

Так как множитель 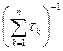не зависит от номера i,то в качестве показателя эффективности стратегии А _i вместо величины (23) можно рассматривать величину:

ā _i =, i =1, …, m . (23)

Оптимальной среди чистых стратегий по рассматриваемому критерию является стратегия с максимальным показателем эффективности (23).

Критерий Байеса относительно рисков при вероятностях состояний природы назовем критерием относительных значений вероятностей состояний природы с учетом рисков. При этом показатель неэффективности стратегии подсчитывается по формуле (6), вероятности q₁ , ..., q_n в которой представлены формулой (2.20.31):

ṝ_i =, i =1, …, m . (24)

Оптимальной среди чистых стратегий по обсуждаемому критерию является стратегия с минимальным показателем неэффективности (24).

2 Алгоритмическое обеспечение

Выбор алгоритма решения задачи зависит от поставленных условий. Если вероятность состояний природы не определена и события равновероятны, то следует остановиться на критерии Лапласа. Если вероятность состояний природы не определена, но события имеют различную вероятность, то следует выбрать критерий относительных значений вероятностей состояний природы. В противном случае следует использовать критерий Байеса. Если исходными данными является платежная матрица, то для решения будут использоваться критерии относительно выигрышей, и критерии относительно рисков для матрицы рисков.

Проиллюстрируем алгоритм принятия решения в условиях риска на конкретном примере с использованием Excel. Для демонстрации всех критериев будем использовать платежную матрицу без заданной вероятности. Рассмотрим 2 случая: события имеют одинаковую вероятность и отличную друг от друга. На основе матрицы выигрышей построим матрицу рисков.

Рассмотрим игру с природой где игрок имеет 7 (m =7) чистых стратегий A₁ , A₂ , A₃ , A₄ , A₅ , A₆ , A₇ , природа П может находиться в одном из четырех (n =5) состояний П ₁ , П ₂ , П ₃ , П₄ , П ₅ . Статистик оценил последствия применения каждой из своих чистых стратегий A_i , в зависимости от состояний П _j природы, результаты представлены в платежной матрице 7×5 (таблица 3).

Таблица 3 – Платежная матрица

A =	П j А i	П 1	П 2	П 3	П 4	П 5
	А1	5	6	4	3	4
	А2	7	4	5	2	3
	А3	2	3	6	4	2
	А 4	4	8	3	0	1
	А 5	4	7	4	6	2
	А 6	7	4	5	2	3
	А 7	1	3	1	1	1