Курсовая работа: Проектирование модели для составления оптимального рациона кормления скота
![]()
ограничения по физической массе силоса
![]()
ограничения по физической массе концентратов
![]()
IV группа ограничений будет иметь экспериментальный характер, задача заключается в том, что, как увеличение ресурсов сена и силоса на 1 кг и концентратов на 3 кг. повлияет на оптимальную стоимость.
ограничения по сену
![]()
ограничения по силосу
![]()
ограничения по концентратам
![]()
V группа ограничений – неотрицательность переменных величин:
![]()
Запишем теперь целевую функцию:
Стоимость рациона должна быть минимальной
![]()
Математическая модель целевой функции имеет вид
![]() (2.3)
(2.3)
где ![]() -стоимость (себестоимость) единицы корма j-го вида.
-стоимость (себестоимость) единицы корма j-го вида.
После построения математической модели пришли к выводу, что заданную задачу целесообразно решать модифицированным симплекс – методом.
3 АЛГОРИТМ МОДИФИЦИРОВАННОГО СИМПЛЕКС-МЕТОДА
При решении экономических задач часто приходится встречаться с такими задачами, у которых ограниченное условие заранее задано равенством и нельзя создать единичную матрицу без проведения дополнительных расчетов. Для решения таких задач используют симплексный метод с искусственным базисом.
1. Привести систему ограничений к каноническому виду.
Если каноническая форма записи не имеет исходного опорного плана, то он строится с помощью дополнительных переменных. Однако независимо от того, используются искусственные переменные или нет, для решения задачи применяется один и тот же алгоритм.
Задача в каноническом виде имеет исходный опорный план
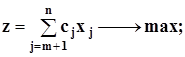 (3.1)
(3.1)
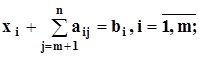 (3.2)
(3.2)
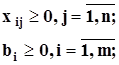 (3.3)
(3.3)
2. Проверить наличие единичного положительного базиса в каждом ограничении.